占丰朝1,2,张小文1,2,闫廷来1,2
1.洛阳双瑞特种装备有限公司,河南洛阳 471001;2.洛阳船舶材料研究所,河南洛阳 471023
摘 要:采用有限元方法对采用不等壁厚设计的无加强U形波纹管轴向刚度进行了非线性分析,并进行了轴向刚度试验,将试验结果、有限元分析结果与推导出的工程经验刚度计算公式进行了对比,验证了有限元分析和工程公式的可应用性,为不等壁厚波纹管的设计开发提供了支持。
关键词:不等壁厚;波纹管;有限元;刚度
波纹管是一种具有补偿位移作用的弹性元件,广泛应用于化工、供热、航天、电力等领域。按波纹管管壁的层数,可分为单层波纹管和多层波纹管。在总厚度相同情况下,多层波纹管相对于单层波纹管具有刚度小、补偿量大、疲劳寿命长等特点,得到了广泛的应用。随着使用工况的严苛,为提高波纹管的耐腐蚀、耐压与高疲劳寿命等综合性能,设计出一种在波纹管接触环境介质侧衬一层高耐蚀合金(如Incoloy825、Incoloy800等)的波纹管,并已在热力、化工产品上有所应用。EJMA—2015《膨胀节制造商协会标准》第9章中对于多层波纹管的应用时指出为了适应管道内外不同的环境,在设计波纹管时允许使用不同的材料制作波纹管的内层和外层,用一层来防腐蚀,其他各层采用价格较为低廉的材料制作;GB/T12777—2019《金属波纹管膨胀节通用技术条件》[1]的5.4.3条给出了不同材料组合的多层波纹管设计温度下的许用应力计算公式。但是针对不等壁厚波纹管的应力计算、刚度计算及性能分析,较少有相关研究。
本文主要通过试验验证和有限元分析来对衬层设计方案的不等壁厚U形波纹管的轴向刚进行研究,以期更好地掌握不等壁厚U形波纹管的轴向刚度,为不等壁厚波纹管的设计开发奠定基础。
01 刚度设计公式
GB/T12777—2019中对于无加强U形波纹管的单波轴向刚度计算公式如式(1)所示。
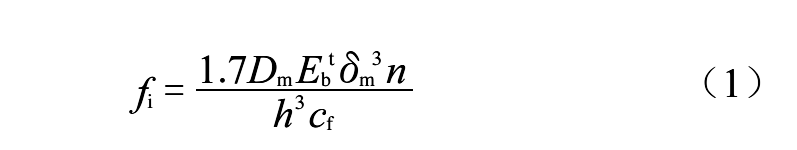
式中各符号意义同GB/T12777—2019[1]。其中n是波纹管的层数,此公式主要适用于各层壁厚相等的多层波纹管的刚度计算,当各层壁厚不相等时,基于并联弹簧刚度叠加原理,并参考等壁厚波纹管刚度计算公式得到不等壁厚波纹管轴向刚度计算公式如式(2)所示:
采用式(2)计算得到的不等壁厚波纹管的刚度数值是否能较好评估不等壁厚波纹管的轴向刚度性能,下文通过有限元分析和刚度试验做进一步验证。
02 有限元分析
2.1 有限元模型和边界条件
针对不等壁厚U形波纹管的轴向刚度性能已有多位学者进行过研究,研究结果表明采用有限元分析方法来研究波纹管的刚度性能是可行的,下文通过有限元分析软件ANSYS Workbench对不等壁厚波纹管的轴向刚度进行分析[2]。
两种不等壁厚方案的波纹管设计参数如表1所示。考虑到后期试验验证成本,这里所衬层波纹管的材质选择跟基层波纹管的材质一样,为耐点蚀性能较好的316L。两种方案不同之处仅在于所衬层的波纹管厚度不同,件号1试验件所衬的一层波纹管厚度为0.5mm,件号2试验件所衬的一层波纹管厚度为1.0mm,基层波纹管厚度均为2.0mm,两个试验件的波高、波距、波根直径等其他参数保持一致。
采用Solidworks软件建立波纹管的三维模型,由于波纹管是轴对称结构,为了减少计算量提高计算效率,这里只建立波纹管的1/4模型,然后将模型导入到ANSYS Workbench中进行分析。考虑到六面体网格可以减少单元数量,加快求解收敛,这里通过扫掠方法生成六面体网格,划分网格后的模型如图1所示。通过查看单元详细信息可以发现模型采用的单元类型对应的名字为Mesh200,这是一个特殊单元类型,并不参与实际的计算,由其对应的Abaqus单元类型名字C3D20,可知相应的有限元单元为Solid 186单元,是一个高阶3维20节点固体结构单元,该单元支持大变形、应力强化、塑性等非线性参数,能够较好模拟非线性行为,因此可以作为非线性分析的有限元单元类型[3]。

300系成型态波纹管的屈服强度与减薄率有关,不同减薄率下成型态波纹管的屈服强度按照如下公式计算[4]。
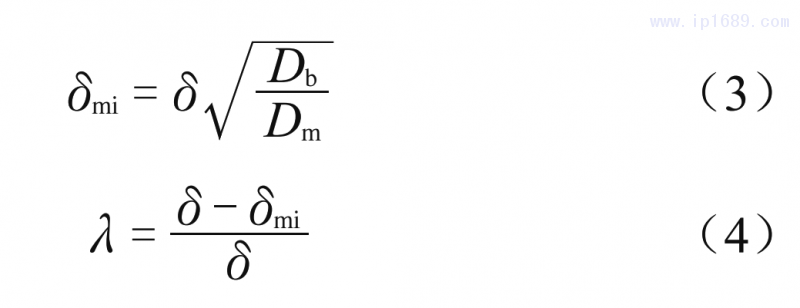
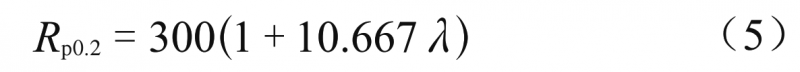
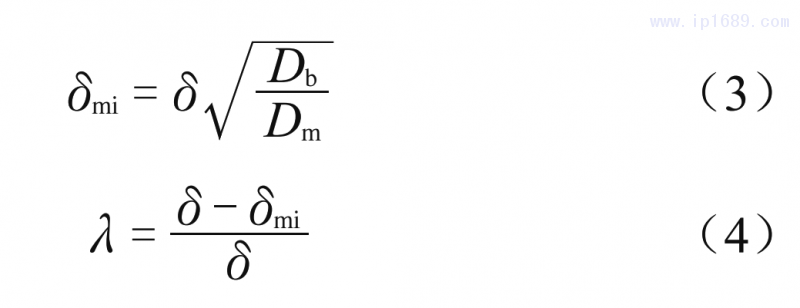
根据表1中波纹管的基本参数,可以得到成型态波纹管材料的屈服强度,成型态波纹管材料的性能参数如表2所示。

波纹管的刚度分析采用的边界条件为一端固支,另一端施加位移载荷。多层波纹管的非线性分析除了考虑材料的非线性行为,还涉及几何非线性和接触非线性。几何非线性通过打开大变形开关来实现,而接触非线性通过设置层与层之间的接触方式来实现,根据现有文献研究波纹管层与层之间比较合适的接触参数可设置为:层间间隙取0.1,法向接触刚度系数取0.1,层间摩擦系数取0.12,通过上述参数的设定来进行非线性分析[5]。
03 刚度试验
为了更好地了解无加强U形波纹管在不等壁厚设计方案下的刚度性能,同时对有限元分析和理论公式计算的结果进行验证,进行了两种设计方案下波纹管的轴向刚度试验。
3.1 试验装置
对于无加强U形波纹管的刚度试验,按GB/T12777—2019规定,实测刚度一般在无压力状态下进行测量,试验前要求波纹管以自由长度置于试验装置内,试验时通过一端固支,另一端施加轴向位移,到力与位移的曲线,由最终的力除以最大位移得到波纹管的实测刚度。
试验装置如图2所示,试验时膨胀节一端固定在试验底座上,底座固定在100T波纹管液压试验机底盘上,另一端通过拉压传感器与试验机上滑块连接,采用液压试验机对试验件施加位移,在试验件上方对称的两个位置各放置一个百分表来记录试验过程中的位移量,通过拉压传感器测量出波纹管的弹性反力反馈给称量显示仪。
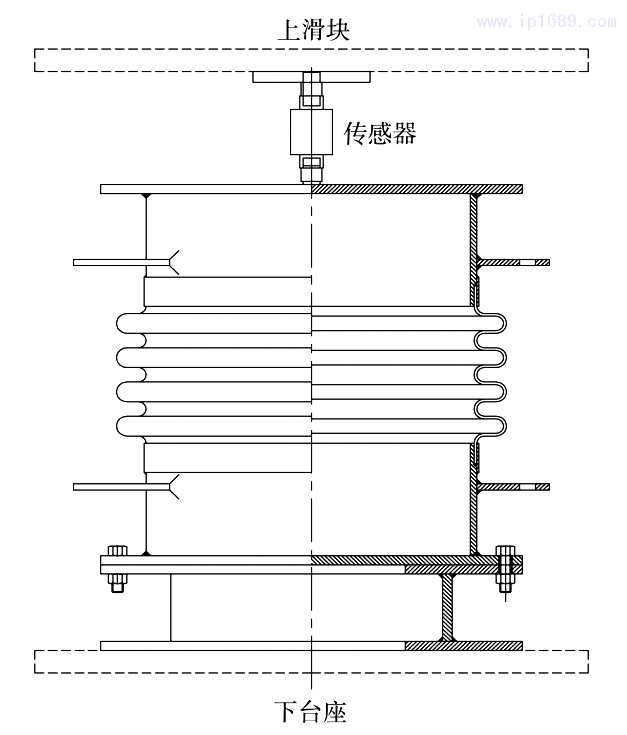
3.2 试验方法
试验时注意保证传感器位于试验件上方中心,为了便于与有限元分析结果作对比,加载过程采用与有限元分析相同的过程,即加载位移为每次增加5mm直至加载至波纹管的设计补偿位移40mm,稳定后记录百分表数值和记录仪读数,由此得到一组力与位移的曲线,为了使试验数据更有说服力,每个设计方案的试验件进行3次测量[6],同时为了更好了解不等壁厚波纹管的轴向刚度性能,分别进行了拉伸位移和压缩位移时的轴向刚度测试。
04 结果分析
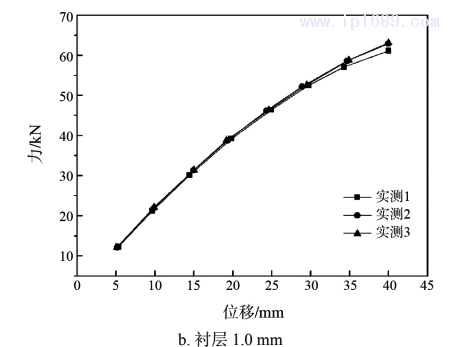
两种设计方案下的试验件测量所得力与位移关系分别如下图3所示,其中图3a所示为内部衬层为0.5mm时,在逐步拉伸到设计补偿位移40mm得到的力与位移关系曲线图,图3b为内部衬层为1.0mm时在逐步拉伸到设计补偿位移40mm得到的力与位移关系曲线图,从图中可以看出,随着位移增大,力逐渐增大,力与位移基本成线性关系。
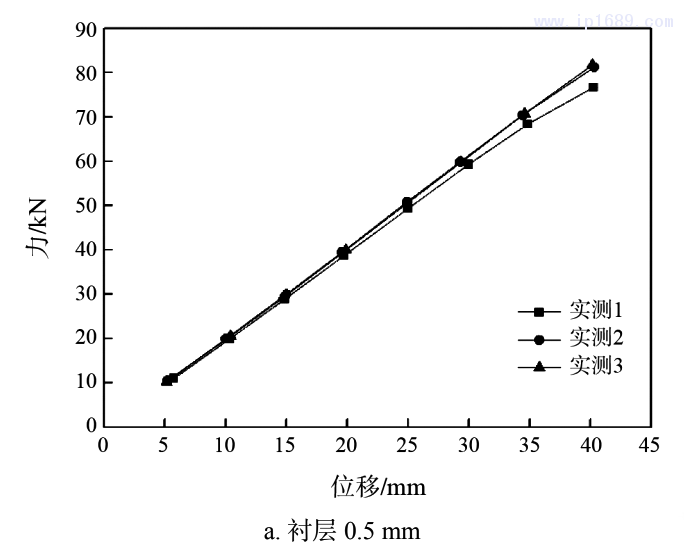
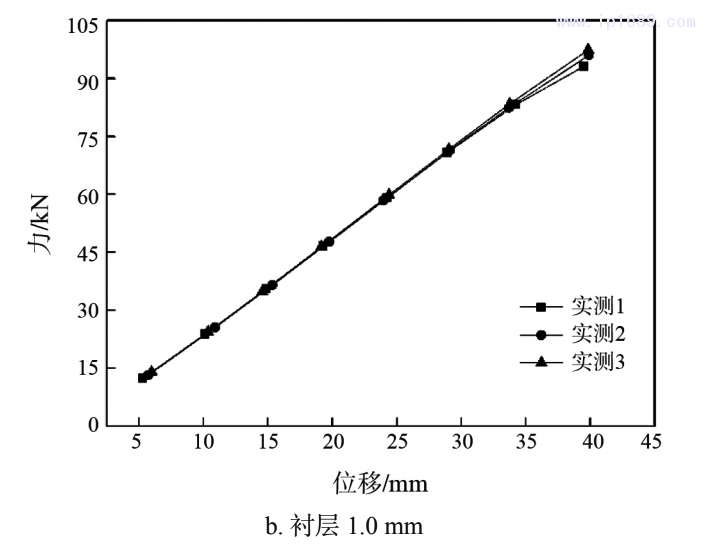
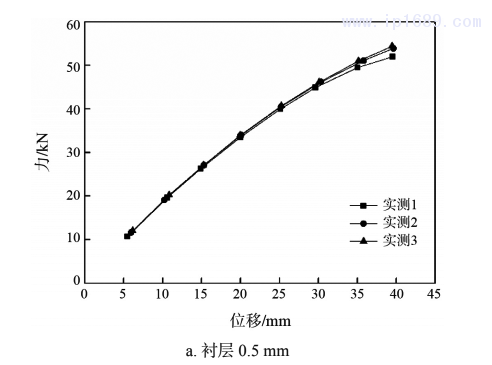
图4为两个试验件在压缩到设计位移40mm过程中的力与位移关系曲线。从图4中可以看到,压缩时波纹管的力和位移的关系为非线 性,从曲线斜率可以看出压缩过程中刚度逐渐减小,此现象与压缩时波纹管的层与层之间作用力增大有关,所衬层的厚度不影响压缩时力与位移变化趋势。
对拉伸得到的实测刚度值和理论刚度值进行对比,结果如表3所示,从表中可以看出理论计算刚度和实测刚度较接近,偏差最大不到20%,由于试验测试时无法保证试验件整体的垂直度,测量刚度值应比实际刚度值偏大,按此原则实际刚度值和理论计算值的偏差会进一步缩小,因此可认为不等壁厚设计时可以按叠加原则进行总的刚度计算,按文中给出的刚度计算公式可以指导工程应用。
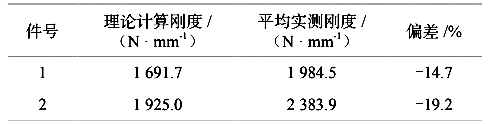
图5为两个试验件通过试验和有限元分析所得到的拉伸到设计位移40mm时力和位移关系对比曲线,其中试验数值为三次试验平均值,从图中可以看到拉伸时有限元分析得到的力和位移的关系与试验测试得到的变化趋势接近。
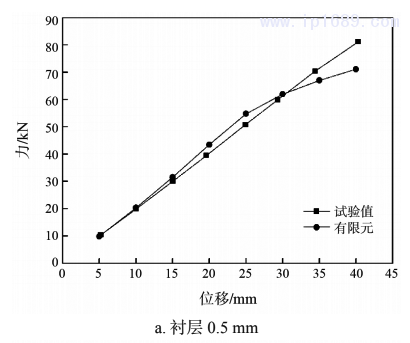
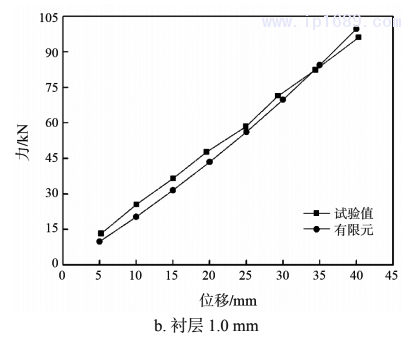
图6为两个试验件通过试验和有限元分析所得到的压缩到设计位移40mm时力和位移关系对比曲线,试验数值为三次试验平均值,从图中可以看到压缩时有限元得到的力和位移的关系跟试验测试得到的变化趋势接近,均为非线性,曲线的斜率逐渐减小。
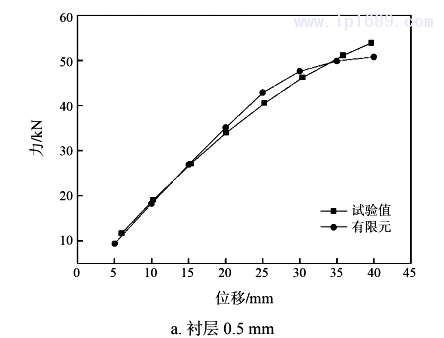
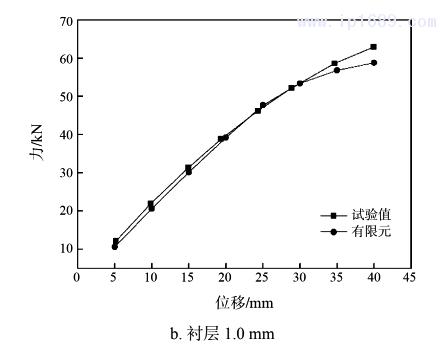
将拉伸时分别经过有限元软件分析计算、理论公式计算及试验测试得到的实测刚度平均值进行对比,对比结果如表4所示,序号1为衬层0.5mm的设计方案,序号2为衬层1.0mm的设计方案,两种设计方案下有限元分析得到的刚度值与实测计算刚度值最大偏差10.4%,相比较于推导出的理论公式计算得到的刚度值更接近实测刚度值,这应与有限元分析时考虑了层与层之间的作用有关,衬层壁厚的增加会使层间作用力增大,因此可以认为采用有限元分析方法来计算不等壁厚波纹管的刚度是可行的,可以一定程度减少试验的数量。

05 结论
通过对不等壁厚U形波纹管进行轴向刚度的试验测试和有限元分析,得出以下结论:
(1)采用文中所示公式对多层不等壁厚U形波纹管的轴向刚度值进行计算分析,计算所得刚度值有较好的精度,但是仍然存在一定偏差,后期可以通过积累更多的不等壁厚波纹管刚度试验结果对计算公式进行修正。
(2)不等壁厚波纹管的刚度进行有限元分析时,在考虑材料非线性和几何非线性的情况下得到的数值与理论值和实测值均接近,通过有限元分析来计算不等壁厚波纹管的刚度是可行的,在对刚度计算值精度要求不高的场合可以进行计算和使用。
本文仅针对两层不等厚度波纹管的轴向刚度进行了分析,多层波纹管在实际使用中,为了满足使用要求经常会采用多于两层的设计,而层数增多时对于有限元分析会涉及更多约束和边界条件,带来的计算结果准确度还有待进一步研究。
符号说明
fi——波纹管单波轴向弹性刚度,N/mm;
Eb——室温下波纹管的弹性模量,MPa;
Ebt——设计温度下波纹管的弹性模量,MPa;
δmi——波纹管成形后一层材料的名义厚度,mm;
δ——波纹管一层材料的名义厚度的数值,mm;
Cf——U形波纹管σ5的计算修正系数;
Dm——波纹管平均直径,mm;
Db——波纹管直边段内径,mm;
Rp0.2——材料的屈服强度,MPa。
参考文献
[1]GB/T12777—2019,金属波纹管膨胀节通用技术条件[S].
[2]王帅,王建军,李楚林等.考虑层间摩擦的多层波纹管轴向刚度非线性有限元分析[J].压力容器,2007,24(12):12-15.
[3]王斌斌.多层波纹管性能的数值分析[C].中国压力容器学会膨胀节委员会.第十五届全国膨胀节学术会议论文集.中国压力容器学会膨胀节委员会.中国机械工程学会压力容器分会,2018:114-124.
[4]陈晔.波纹管的平面稳定性研究[D].南京:南京工业大学博士论文,2011.
[5]李杰,段玫.多层波纹管接触分析及稳定性屈曲分析[J].材料开发与应用,2011,26(6):53-57.
[6]刘岩,段玫.蝶形金属波纹管的轴向刚度研究[J].压力容器,2007,24(1):8-11.









 玻纤含量对长玻纤...
玻纤含量对长玻纤... 钙钛矿薄膜的均匀...
钙钛矿薄膜的均匀... 用于光伏板静电除...
用于光伏板静电除... 聚砜医疗干粉吸入...
聚砜医疗干粉吸入...













