赵毅，刘淑梅∗，潘泓谊
（上海工程技术大学材料工程学院，上海 201620）
摘要：为降低某报警器上盖注塑的翘曲变形，课题组在分析不同尺寸浇口的翘曲量和剪切力结果后，选用了较优的１.３ｍｍ浇口。在此基础上建立了响应面方案，对工艺参数进行优化。选择注塑时间、保压时间和保压压力为优化参数，以翘曲量为响应目标，利用Moldflow进行模拟，结合Design Expert软件对方案结果进行分析，利用回归方程拟合预测值。得到了最优工艺参数为：注塑时1.5ｓ，保压时间9.6ｓ，保压压力70MPa。根据最优方案获得了合格的产品，证明了优化结果的可靠性。
关键词:注塑成型；翘曲；响应面法；Moldflow；Design Expert
报警器在汽车领域有许多应用，本课题研究的报警器在车速低于30km/h时，会模拟发动机引擎的声音来提醒行人，属于车辆低速报警器。通常报警器壳体为注塑件，壳体内部装载电子系统，因此壳体上盖需要与底座紧密配合，确保良好的密封性，以保护其内部系统不受腐蚀。基于此，注塑时尽量减少翘曲以降低尺寸误差。王桂龙等[1-3]发现在盖类零件的注塑过程中影响较大的工艺参数有保压压力、注射时间和保压时间，其余参数影响较小。此外，对于工艺参数的优化，响应面法可以根据参数指定范围内的样本点和测试结果，拟合目标和参数的线性回归方程，根据方程预测最优参数组合；响应面法精密度高、预测性能好，比较适合做工艺参数的优化设计[4-5]。课题组结合前人的研究成果，在数值模拟的基础上建立响应面方案，研究注射时间、保压时间和保压压力对报警器上盖翘曲变形的影响，通过实际生产和产品测试证实了优化结果的可靠性。
1 工艺分析
报警器上盖的结构如图１所示，所用材料为PBT+PC，含有质量分数为15%的玻纤，牌号为Pocan B 7616。由于具有优良的耐热性能、电气性能和阻燃性能以及吸水率低的优点，该种材料常用于电子电器设备中。
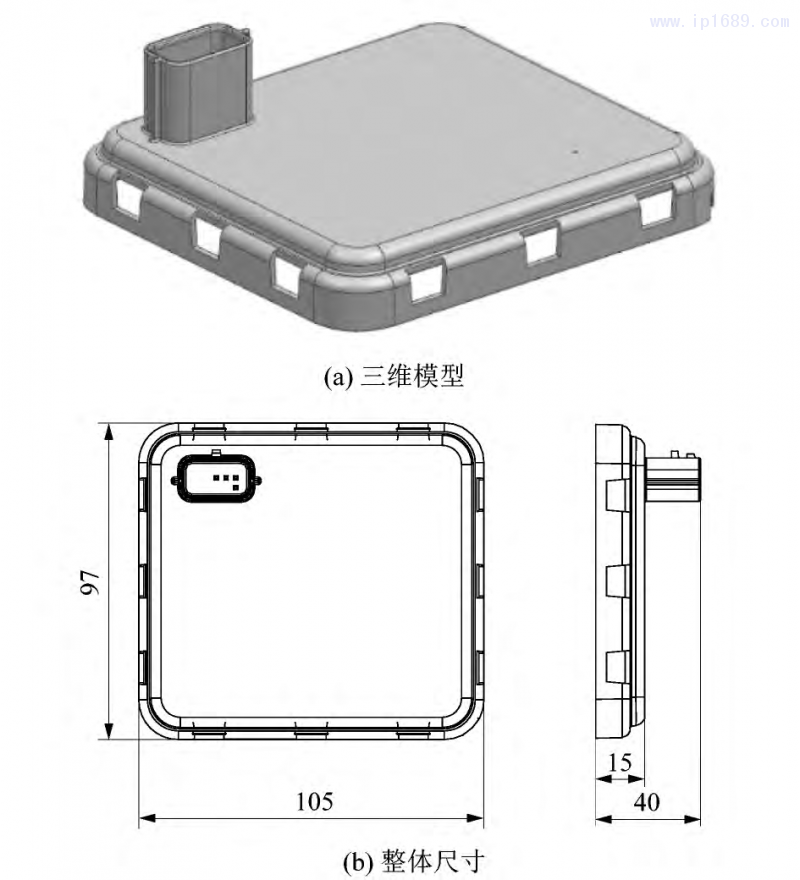
由图１可以看出，报警器上盖长105ｍｍ，宽97ｍｍ，是典型的方盒件。在其注塑成型过程中，模具结构是影响翘曲的关键因素之一，该报警器上盖形状规则，尺寸居中，出于模具成本考虑，采用单浇口，结合Moldflow的浇口位置分析，最终选用中心点浇口注塑。注塑过程中浇口尺寸过大会导致熔料各向异性增大，垂直料流方向的收缩率变大；浇口尺寸太小会导致浇口处的剪切速率和剪切应力变大，导致塑料断层，影响产品性能［６］。课题组采用点浇口注塑，设计了４个浇口尺寸，分别为1.0，1.3，1.5和2.0 ｍｍ。采用相同的工艺参数仿真模拟，观察４个方案对于产品性能的影响。各浇口尺寸对应的翘曲量和剪切应力如表１所示。
对比发现，采用1.0和1.3ｍｍ浇口产生的翘曲较小，但根据材料注塑性能，材料允许的最大剪切应力为0.4 MPa，1.0ｍｍ浇口的剪切应力为0.416 MPa，超过了临界值，所以考虑选用1.3ｍｍ浇口尺寸。
２基于响应面法的参数优化
２.1设计变量和响应目标
工艺参数对不同类型零件翘曲影响有差异，根据前文分析，在报警器上盖成型优化中，挑选注射时间Ａ、保压时间Ｂ和保压压力Ｃ３个参数作为优化对象，翘曲量Ｄ作为响应值。由成型窗口分析的质量填充发现，在0.3～2.8ｓ内可以完成注塑，因此选取注射时间为0.5～1.5ｓ，保压时间为4.0～12.0ｓ，保压压力为50～70MPa。各工艺参数的取值范围如表２所示。
2.2建立响应面方案
响应面法（RSM）是一种将数学方法和统计方法相互联系，根据试验方案的样本点，建立试验变量与响应值之间函数关系的方法。响应面法有BBD（box behnken）和CCD（central composite design）两种试验设计方法，CCD会选出超出参数范围的样本点，可以更好地拟合响应曲面[7-8]。因此课题组采用中心复合响应面设计方法（CCD）进行优化设计，根据Design Expert中的CCD设计方案，试验因素水平表如表３所示，－α和＋α分别表示各因素超出上下限范围的样本点。
将参数范围输入到Design Expert软件中，生成CCD设计方案并进行试验模拟，表４所示为试验方案和翘曲量（响应值）结果。
３试验结果分析
３.1回归方程拟合
基于表４的样本点和响应结果，采用二阶方程拟合翘曲量Ｄ与注射时间Ａ、保压时间Ｂ和保压压力Ｃ之间的回归模型，公式为
D=0.424+0.142A+0.013B+5.353×10-4C+3×10-3AB-1.9×10-3AC-1.437×10-4BC-0.021A2-3.339×10-4B2-7.745×10-6C2｡ (1)
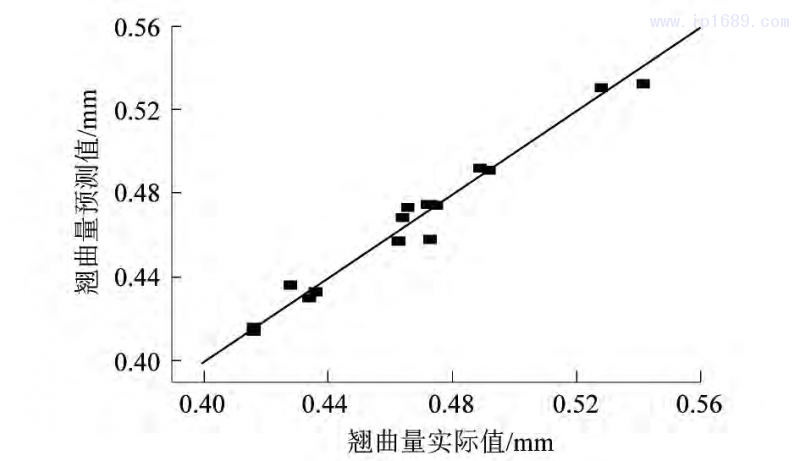
Design Expert可以根据拟合的回归方程预测翘曲响应值，图２为报警器上盖翘曲的预测值和实际模拟值的离散对比图，以翘曲量实际值作为离散点。由图２可知，预测值与实际模拟值较为接近，由此说明该响应面模型的准确度较高，可以准确预测报警器上盖的翘曲量。
３.2响应曲面分析
为了更直观地分析因素之间的交互作用，通过响应曲面图来观测因素之间对目标的影响。图３为响应模型的三维曲面，反映了３个因素交互作用对翘曲量的影响。由图3(a)可以看出，当保压时间Ｂ不变时，翘曲量随着注射时间的减小有所降低，因为注射速率增大，可以减少残余应力的堆积。由图3(b)和3(c)可以看出，当注射时间Ａ和保压时间Ｂ不变时，翘曲量随着保压压力Ｃ的增大而减少，是由于保压压力高可以使补料充足，从而减少收缩和翘曲［９］，响应曲面的趋势和实际预测基本一致。
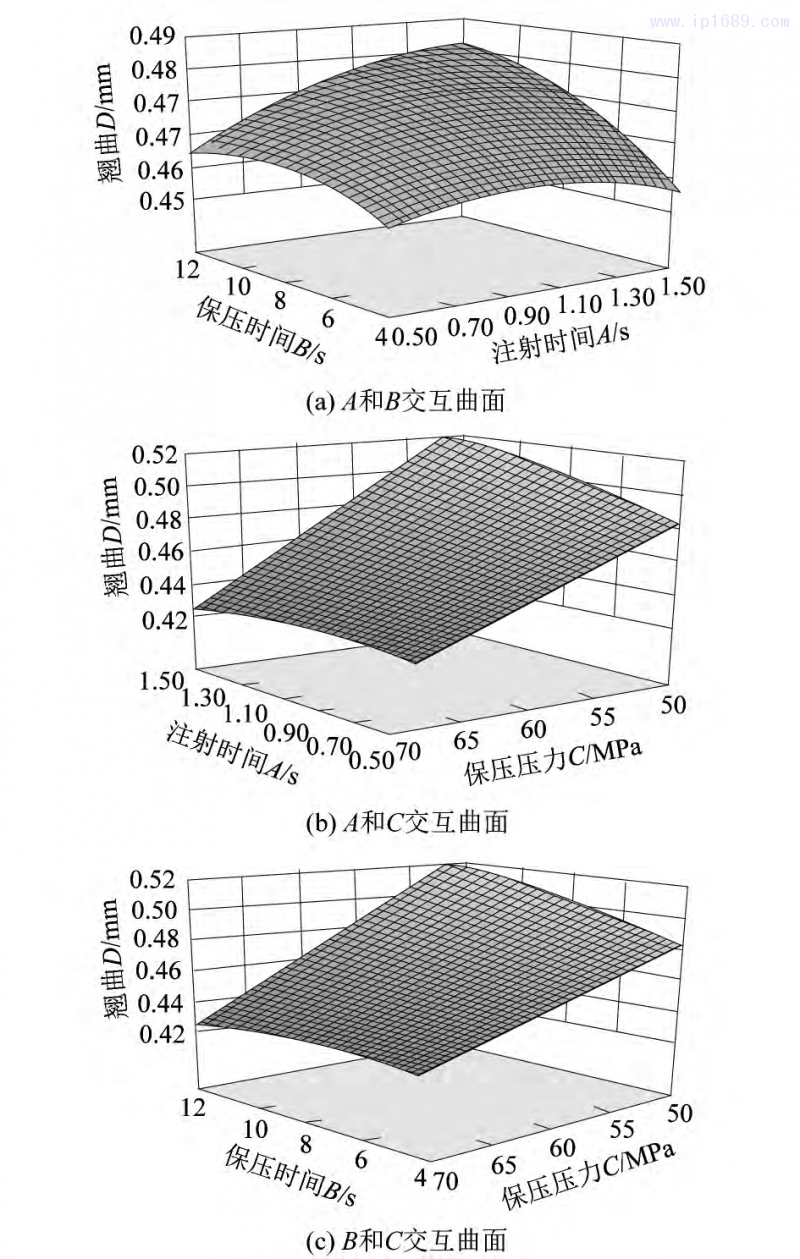
表５为翘曲量响应模型的方差分析表。其中，模型Ｐ值越小代表模型对响应值的影响越显著，Ｐ值小于0.05时表明为显著项，大于0.1时为非显著项。由此可以判断，Ａ，Ｂ，Ｃ，ＡＢ，ＡＣ和Ａ２为显著项，其余为非显著项。此外，模型相关系数Ｒ２＝87.3％，表明响应面模型的拟合程度良好，校正系数为94.6％，说明只有5.4％的响应值不能用此模型来解释。本模型的信噪比为22.42（大于４即是合理的），证明模型的分辨能力良好[10]。
４试验结果验证
４.1模拟验证
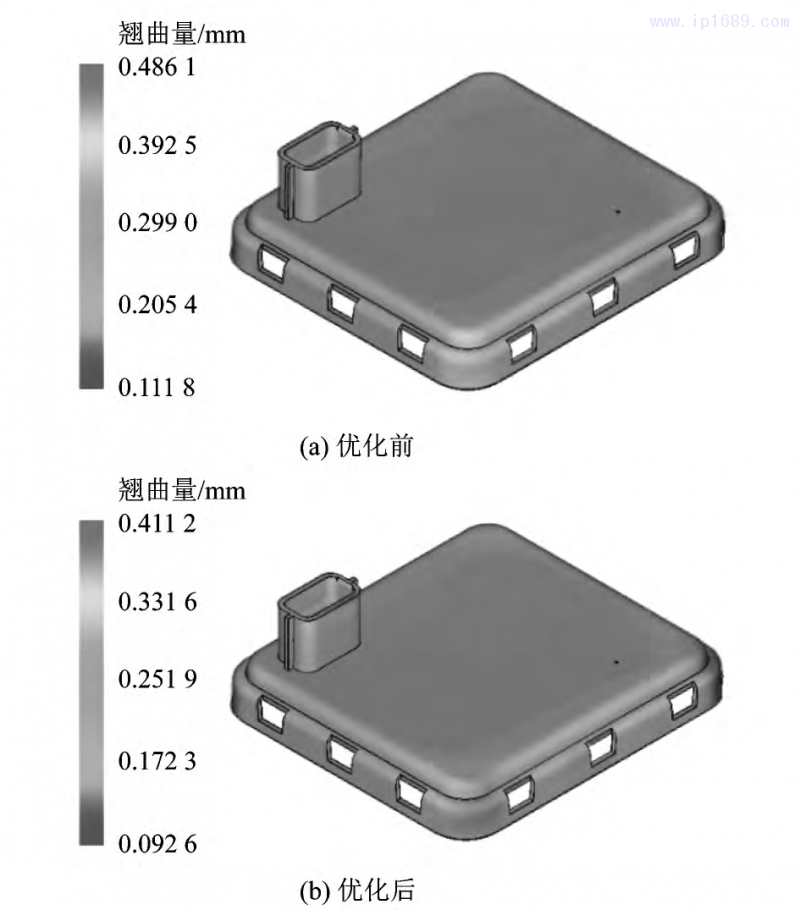
以最小翘曲量为期望目标，通过Design Expert软件可以预测报警器上盖的最优工艺参数，即注射时间为1.5ｓ，保压时间为9.6ｓ，保压压力为70MPa，翘曲量的预测值为0.4092 mm。重新利用Moldflow软件对该组合进行仿真分析，模拟的翘曲结果为0.4112ｍｍ，与优化的预测值较为接近，说明最优参数组合的选取比较合理。图４为工艺参数优化前后的最大翘曲量对比。由图４可以看出，与最初方案的翘曲量０.4861ｍｍ相比，优化后的翘曲量降低了１5％。
4.2生产验证
为了验证优化结果的可靠性，采用最优工艺参数组合生产报警器上盖，图５为试生产的样品。经过三维尺寸测量，产品实际翘曲变形与模拟结果相似。同时优化的目的是提高上盖与底座配合的可靠性，将产品与底座装配后进行-40～＋105℃、60min的温度循环，随后浸入40℃水中进行防水测试，结果显示无泄漏，说明经过温度循环后产品没有出现较大变形，仍具有良好的防水性，由此判定产品质量合格。
５结语
课题组对报警器上盖的注塑方案进行分析，对比不同尺寸浇口的翘曲量和剪切应力，后采用了1.3mm浇口，发现产品翘曲小，剪切应力适中。在此基础上，设计响应面优化方案，结合前人分析经验，选择注射时间、保压时间和保压压力进行参数优化，期望减少产品翘曲，通过回归模型的预测得到了最优工艺参数组合：注射时间为1.5s，保压时间为9.6s，保压压力为70MPa。利用Moldflow对最优工艺参数进行模拟，结果证明优化后的产品翘曲降低了15％。同时，将最优工艺参数组合用于指导样品生产，得到的产品尺寸测量结果符合预期。经过测试产品温度循环和防水性能，确认产品质量合格，验证了优化结果的可靠性。
参考文献：
［１］王桂龙，赵国群，李辉平，等．薄壁注塑制品翘曲影响因素分析与工艺优化［Ｊ］．中国机械工程，2009，20(4)：488-491.
［２］周应国，申长雨，陈静波，等．工艺参数对注塑制品翘曲影响的CAE分析［Ｊ］．工程塑料应用，2006，34(11)：28-31.
［３］张继祥，秦海涛，钟厉，等．薄壁件注塑翘曲变形综合优化分析［Ｊ］．塑料工业，2014，42(5)：56-61.
［４］李莉，张赛，何强，等．响应面法在试验设计与优化中的应用［Ｊ］．实验室研究与探索，2015，34(8)：41-42.
［5］MASON R L，GUNST R F，HESS J L. Statistical design and analysis of experiments with applications to engineering and science[M]. New York:John Wiley and Sons Publication，2003:568 - 586.
［６］赵永成，吴亚南，董淑婧．注塑成型收缩率影响因素的分析［Ｊ］．塑
料工业，2005，33(12):30 - 31.
［７］张静，郭竞宇，梁颖，等．基于响应面法的单座阀阀杆预锻工艺优化[J]. 轻工机械，2017，35(5):66 - 68.
［８］ 程敬丽，郑敏，楼建晴．常见的试验优化设计方法对比［Ｊ］．实验室研究与探索，2012，31(7):10-11.
［９］ 秦欣，苏小平，郭存涵．基于响应面法的汽车保险杠注塑方案分析与优化［Ｊ］．塑料科技，2019，47(2):60 - 61.
［１０］ 卢松涛，王培安．基于响应面法和正交试验的墨顶盖翘曲变形优化［Ｊ］．塑料，2020，49(4):67 - 68.
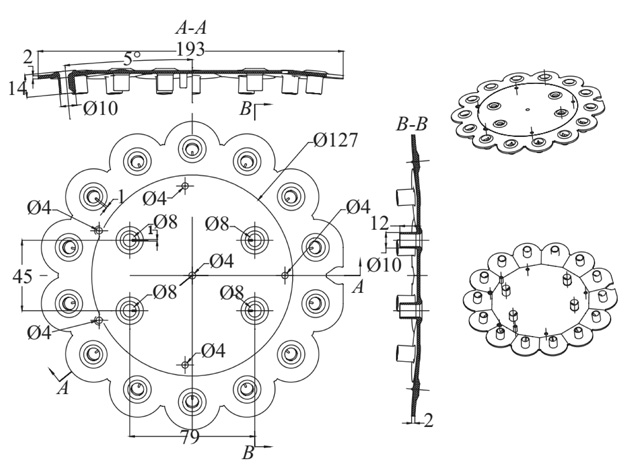聚砜医疗干粉吸入...
塑料包装材料的减...
汽车功能键触摸盖I...
高性能注塑聚丙烯...
