刘永兴1 唐小琦1 钟靖龙1 钟震宇2 周向东1
1.华中科技大学机械科学与工程学院,武汉,430074
2.广东省科学院智能制造研究所,广州,510070
摘要:受温度、气压等环境不稳定因素的影响,注塑成形加工过程中工艺参数发生变化,从而导致产品精度下降,产品降级或报废。针对类似环境不稳定因素影响问题,利用加工过程中的数据进行注塑成形尺寸预测,有助于不合格产品的及时发现,减少不合格品的产生。基于轻量级梯度提升机(LightGBM) 框架设计了基于加工过程数据及参数的注塑成形产品尺寸预测模型,通过特征提取、异常数据处理、数据集划分、模型训练、模型验证等步骤,建立了具有非对称风险特征的产品尺寸预测模型。针对产品尺寸超规的非对称风险问题,在模型训练过程中引入了基于尺寸范围的加权修正方法,以提高预测模型对超规尺寸的预测精度。最后利用富士康注塑成形尺寸预测数据集进行了验证,结果表明,该模型对超规尺寸具有更高的预测精度,尺寸预测结果平均误差为0.015 mm,考虑非对称风险的加权平均误差为5×10-6 mm。
关键词:注塑成形;非对称风险;机器学习;尺寸预测;轻量级梯度提升机
引言
注塑成形作为一种常见的加工工艺,具有生产速度快、效率高、自动化程度高 、产品尺寸范围广、制品精度较高、产品易更新换代等优点,适用于大量生产形状复杂产品的成形加工领域[1]。但注塑成形加工过程复杂且对环境较为敏感[2],加工过程中的环境温度、气压 、冷却水温度等不稳定因素容易造成产品精度下降、尺寸超规,从而导致产品降级或报废[3]。为提高加工精度,ZHOU等[4]使用压力积分作为特征,建立了一种基于聚合物熔体性能的质量预测模型,实现了在线监测产品重量变化。ZARGES等[5]利用机器学习方法建立了注塑加工流程的仿真模型,实现了注塑产品长度尺寸的预测,与实验结果对比发现仿真模型具有较高的精度。目前,工业应用中更加关注超规尺寸的预测精度,上述研究实现了注塑成形的产品质量预测,但未关注实际注塑成形生产中产品尺寸的非对称风险问题,造成对样本量较小的超规尺寸产品的预测能力较差。
为提高预测模型对少样本超规尺寸产品的预测精度,本文利用注塑加工过程数据,基于轻量级梯度提升机(light gradient boosting machine,LightGBM) 算法框架建立了注塑成形尺寸预测模型,并针对注塑成形产品尺寸超规的非对称风险问题,设计了基于尺寸界限的权重修正方法。在富士康注塑成形尺寸预测数据集上实现了对非对称风险条件下的注塑成形产品尺寸预测模型的验证,验证集结果表明该预测模型对超规尺寸和危险尺寸区域的尺寸预测具有更高精度。
1 注塑成形工艺及数据分析
1.1 注塑成形工艺流程
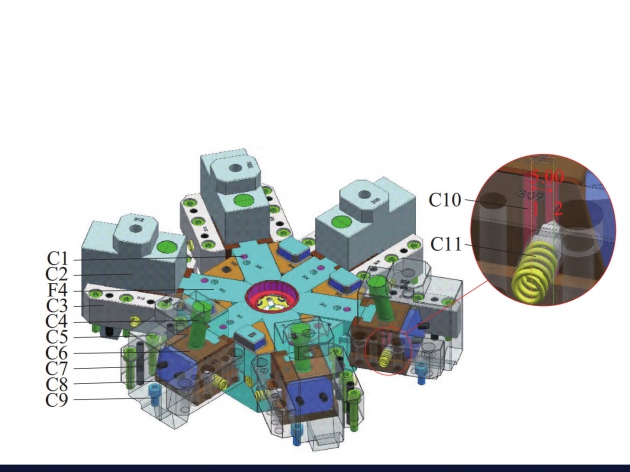
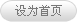
注塑成形工艺是通过注塑机将熔融的原料压入成形模具中,经过加压、注入、冷却、脱模等一系列操作制作成一定形状的半成品塑料制品的工艺过程,具有多阶段复杂流程。注塑机的结构如图1所示,在工作过程中通过螺杆或柱塞等部件的推力,将经过加热器塑化的熔融状态(即黏流态)的塑料注射入闭合的可分离模具腔体内,经过一定时间的保压固化后脱模获得塑料制品。注塑成形工艺流程包括定量加料、加热塑化、加压注射、保压冷却、启模取件,如图2所示。
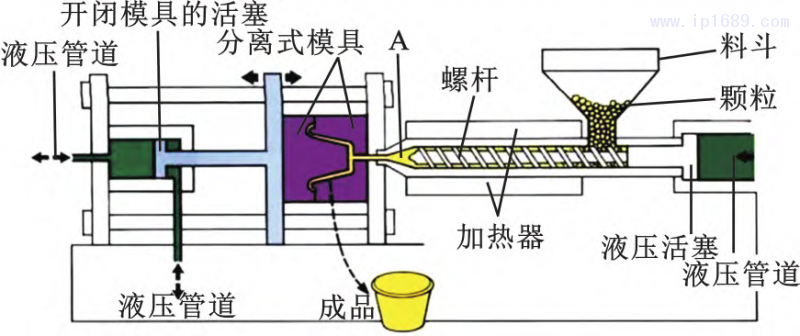
图 1 注塑机结构原理
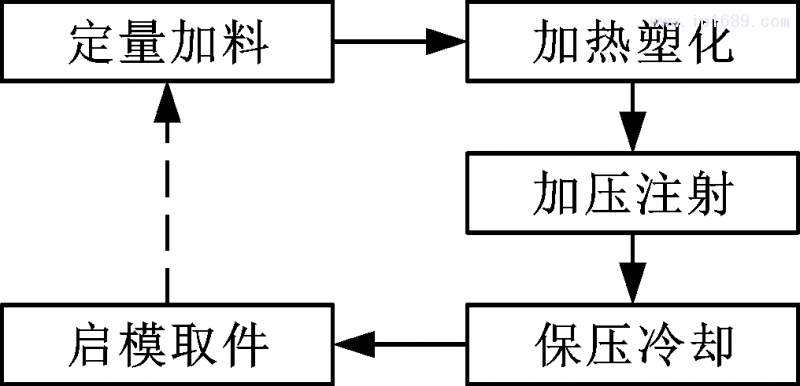
图 2 注塑循环流程
1.2 注塑成形尺寸预测数据集
本文中所使用的注塑成形尺寸预测数据集[6]由富士康工业互联网股份有限公司发布,包括16600个数据样本,记录了传感器高频数据、成形机状态数据,以及每个加工模次对应的产品3个特征的测量尺寸(尺寸1、尺寸2、尺寸3),数据具有样本量大、维度高的特点。其中各类数据含义如下:
(1)传感器高频数据。传感器高频数据是模温机及模具传感器采集的数据,单个产品加工时长为40~43s,采样频率根据阶段有20Hz和50Hz两种,含有24个传感器采集的数据。
(2)成形机状态数据。成形机状态数据是注塑成形过程中的一些状态数据,其数据维度为86维。
(3)产品测量尺寸。产品测量尺寸含有每个产品3个特征的尺寸数据。
2 非对称风险尺寸预测模型
针对注塑成形加工中的尺寸预测,本文提出的非对称风险下尺寸预测模型的建模流程如图3所示,主要分为六大步骤:高频数据特征提取,数据处理,数据集划分,非对称风险处理,模型训练,模型验证。
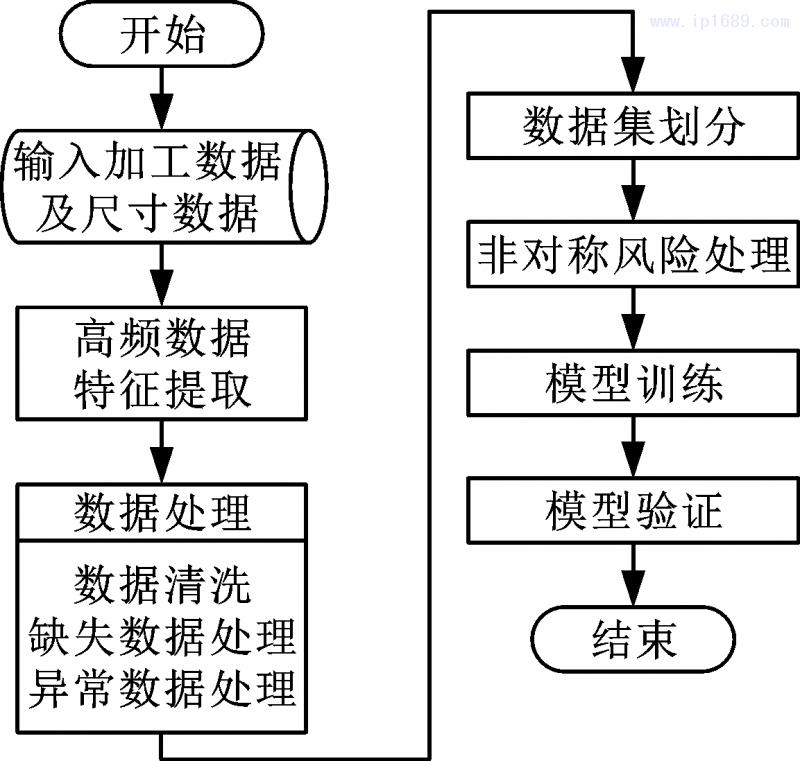
图 3 尺寸预测模型建模流程图
2.1 高频传感数据特征提取
借助python平台对注塑成形尺寸预测数据机中的传感器高频数据及加工阶段绘制基于时间的折线图并进行可视化分析。图4为某个加工模次中关键传感器数据曲线图,可以看出,3个压力传感器在加工过程中采集到的压力数据随加工时间、加工阶段不断变化,由此可以反映出加工过程中设备的运行状态。
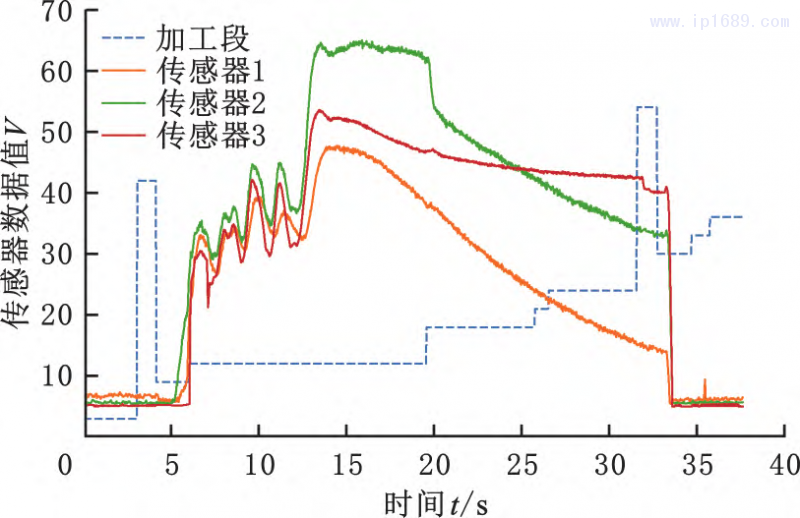
图 4 单次加工压力传感器高频数据图
在注塑成形加工过程中,通过安装在设备上以及环境中的共24组传感器采集到大量的高维高频数据,单个产品加工时长为40~43s,采样频率分阶段有20Hz或50Hz,单次生产采样次数约1600,则单次生产采集的数据量约为24×1600,为提高模型的计算效率,需要提取数据中的有效特征,降低数据维度。
由于注塑成形工艺特征复杂,各传感器数据的重要性无法在特征提取阶段确定,因此本文对高频数据提取多种特征以充分反映加工过程中设备状态对产品的影响,提取的15种特征包括均值、最大值、最小值、中位数、方差、多个分位值等。通过特征提取方法,将高频数据维度降维到 360(24×15)个特征值。
2.2 尺寸预测的非对称风险处理
2.2.1 尺寸预测的风险不对称
由于产品尺寸容许一定的误差,尺寸超出误差范围时需要报废或降级,因此产品尺寸预测的风险不对称,需要在尺寸超规的情况下具有更高的预测精度。本文针对注塑成形加工中的非对称风险问题进行处理,如图5所示,将尺寸数据根据尺寸上下限分为6个区域,可以分类为三种尺寸:安全尺寸、危险尺寸、超规尺寸。非对称风险尺寸预测模型中,三个尺寸区域的尺寸预测精度要求不同,安全尺寸区域(区域3、4) 的预测精度要求较低,超规尺寸区域(区域1、6)的预测精度要求最高,危险尺寸区域(区域2、5)的预测精度要求居中。
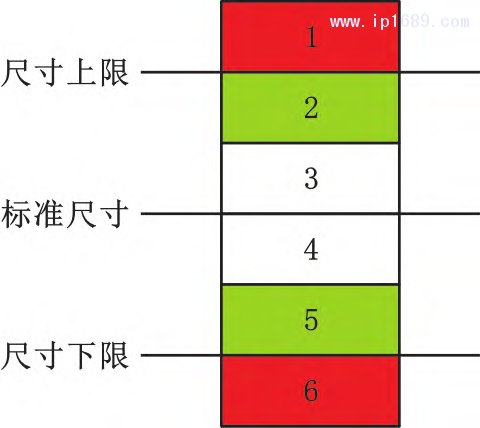
图 5 尺寸区域非对称风险的分区图
2.2.2 超规风险损失函数加权修正
常规尺寸预测模型中的损失函数以尺寸预测精度为目标,标准损失函数形式为
L(φ) = ∑l(yni ,yi ) (1)
式中,yni为单棵决策树对第i个样本的预测值;yi为第i个样本的真实值;l(yni,yi ) 表示决策树的损失函数。
产品尺寸超规后需要降级或报废重塑,这会降低产品合格率、增加生产成本,所以不同尺寸区域的风险不同,危险/超规尺寸区域需要更加精确的预测。训练过程中,由于样本数量差异,超规尺寸与危险尺寸区域的样本占比较小,安全尺寸区域样本在模型训练中累计的损失占主导地位,造成模型对安全尺寸区域的预测更加精准,这与本文研究的注塑成形尺寸预测模型的目标不符。
本文针对上述风险不对称、样本不均衡情况引入样本权重数据,依据训练尺寸与尺寸界限确定样本权重,同时使用L2损失函数降低过拟合风险,其表达式为
L(φ) = i l(yni ,yi ) (2)
式 中,ai 为第i 个样本对应的超规风险的加权系数。
损失函数采用基于预测误差平方和最小化的L2损失函数,其表达式为
L2LossFunction = ∑ (y - y ) 2 (3)
i=1
式 中,y 为第i 次加工预测目标的真实值;y 为第i 次加工预测目标的预测结果;n 为总加工次数。
2.3 LightGBM 模型
本文采用基于决策树算法的轻量级梯度提升机(LightGBM) [7]作为算法框架。LightGBM模型采用直方图算法(图6)、带深度限制的按叶生长策略(图7)等改进方法,使得该模型训练速度相对于梯度提升机(GBM) 模型和XGBoost模型得到了显著提高。在工业大数据应用场景中,面对大样本、高维度的工业数据集时,LightGBM模型具备较快的训练速度,有利于随生产过程进行迭代升级。
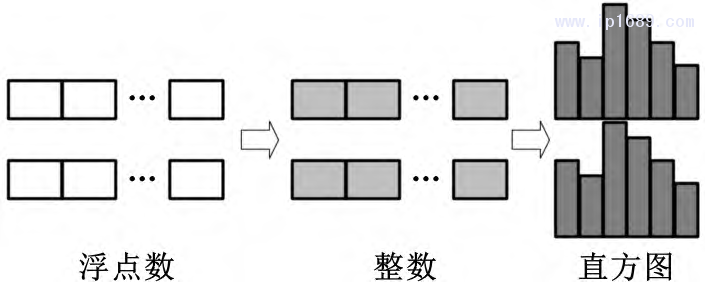
图 6 直方图算法示意图
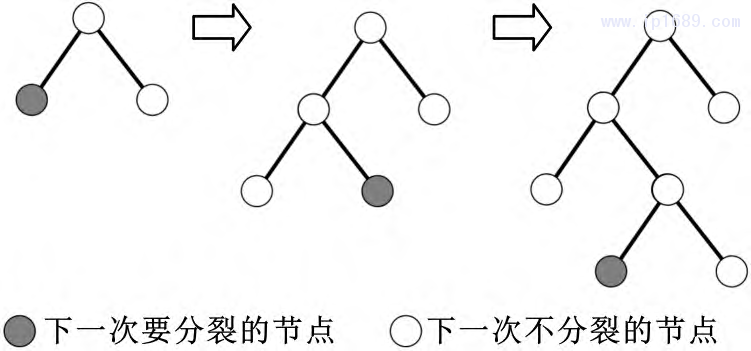
图 7 按叶生长策略示意图
3 模型训练及验证
3.1 异常数据处理
在模型训练过程中,异常数据对模型训练过程会造成较大影响。本文采用基于局部的模型异常数据处理方法判定异常数据,并删除异常数据。在注塑成形数据集中,由于加工过程中的调试、数据记录错误等原因,存在部分异常数据,如图8中标记的异常数据严重偏离邻近尺寸数据的均值,需将这些异常数据进行删除处理。
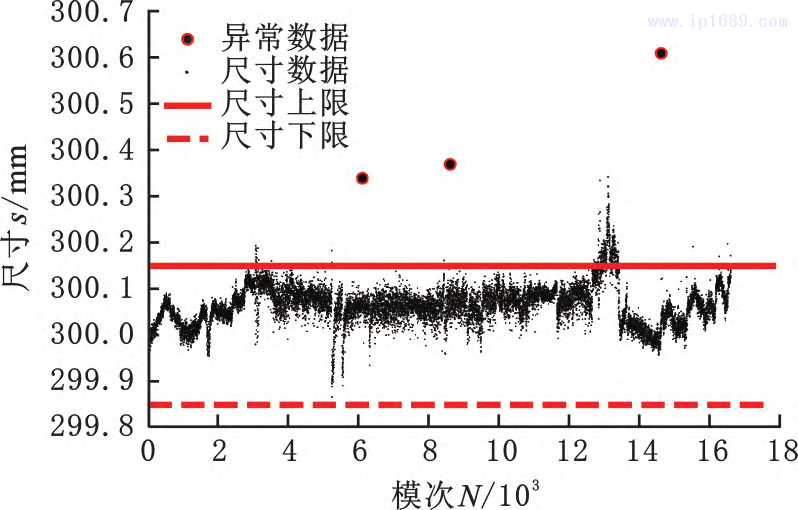
图 8 异常数据的标注
3.2 数据集划分
为验证注塑成形尺寸预测模型的准确性,将数据集分为两部分:训练集与验证集。训练集用于模型训练和超参数调整,验证集用于估计模型的泛化误差。将80%的数据作为训练数据,20%的数据作为验证数据。该数据集共有数据16600模次,异常数据3模次,13277模次数据作为训练集数据,3320模次数据作为验证集数据。
3.3 超规风险损失权重
针对不同尺寸的尺寸界限不同以及注塑成形的尺寸要求,设计了非对称超规风险下的尺寸权重处理函数。如表1所示,三个尺寸的尺寸要求不同,每个尺寸的加权数据需要独立处理。超规风险的加权函数如下:
ai = (ekw + 1) 2 (4)
e =| yi - y s|
式 中,e 为样本尺寸与标准尺寸的差值;k为尺寸上下限决定的比例系数;w 为不同区域的修正系数;y s 为样本的标 准值;lu 尺寸上界;ld 为尺寸下界。
表 1 尺寸标准值及误差范围
尺寸 1 尺寸 2 尺寸 3
标准尺寸 y s 300.000 200.000 200.000
尺寸上界 lu 300.150 200.075 200.075
尺寸下界 ld 299.850 199.925 199.925
3.4 模型训练
基于LightGBM框架实现尺寸预测模型的构建,在模型训练中,对训练集数据使用五折交叉验证方法(图9),以提高训练集数据的泛化能力。LightGBM训练参数如表2所示。图9中,D表示数据,本文将其划分为D1~D5五个部分。
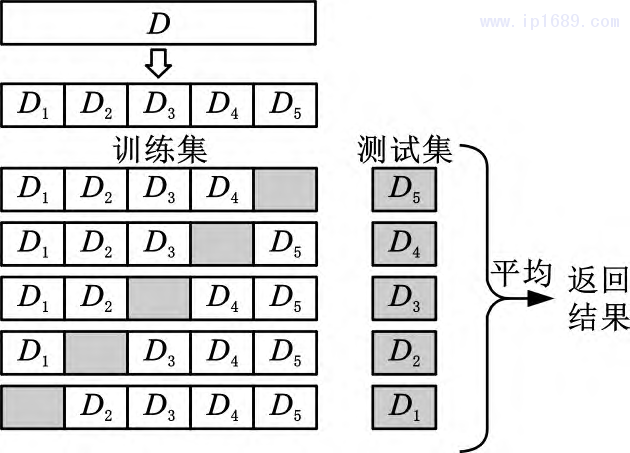
图 9 五折交叉验证方法
表 2 LightGBM 训练参数表
精度提升算法 梯度提升树(GBDT)
损失函数 L2 损失函数
叶子数 511
学习速率 0.1
最大迭代次数 5000
提前停止次数 50
3.5 实验结果与分析
在富士康注塑成形尺寸预测数据集上进行实验,本文提出的非对称风险尺寸预测模型的预测结果如图10所示,可以看出,预测结果与原始尺寸的分布趋势接近。
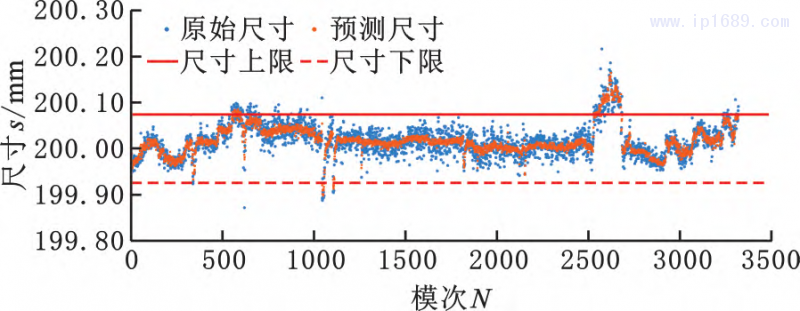
( a) 尺 寸 1
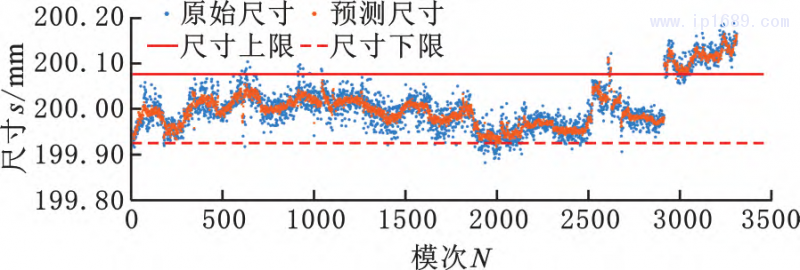
(b) 尺 寸 2
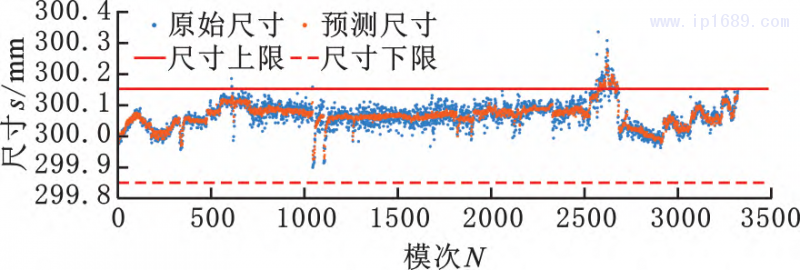
( c) 尺 寸 3
图 10 尺寸预测结果分布
表 3 预测结果误差
误差项 尺寸 1 尺寸 2 尺寸 3 总误差
尺寸误差范围 ±0.15 ±0.075 ±0.075
平均误差 1.34×10-2 1.46×10-2 1.26×10-2 0.015
误差标准差 1.25×10-2 1.21×10-2 1.05×10-2 0.013
加权平均误差 4.79×10-6 4.67×10-6 4.89×10-6 5×10-6
加权误差标准差 1.77×10-5 1.03×10-5 1.94×10-5 2×10-5
对预测结果的误差统计如表3所示,三个尺寸的误差范围为±0.15mm、±0.075mm,总误差为考虑三个尺寸误差保留1~2位有效数字的不确定度数据,其中预测结果平均误差约0.015mm,预测精度较高,考虑非对称风险的加权平均误差达到5×10-6mm,表明本文设计的非对称风险尺寸预测模型在尺寸超规或接近尺寸界限时具有更高的预测精度,符合尺寸预测模型的设计目标。
4 结论
(1) 对注塑成形加工过程中采集的高频数据进行可视化分析,使用多种特征提取方式对高维度加工数据提取特征,保留了高频数据中的关键信息,降低了数据维度,提高了模型训练效率。
(2) 考虑注塑加工中尺寸超规的非对称风险,引入了基于尺寸界限的权重参数,调整了不同尺寸在训练集中的权重,使得尺寸预测模型对超规尺寸/危险尺寸更加敏感,提高了预测模型对超规尺寸/危险尺寸的预测能力。
(3) 在富士康注塑成形尺寸预测数据集上进行实验,结果表明,本文提出的非对称风险尺寸预测模型的尺寸预测平均误差约0.015mm,考虑非对称风险的加权平均误差约5×10-6mm,实现了注塑加工中的尺寸预测,对超规尺寸/危险尺寸具有更高的预测精度,具有一定的工程应用价值 。
参考文献:
[1] CHEN J Y ,TSENG C C ,HUANG M S.Quality Indexes Design for online Monitoring Polymer In-jection Molding[J].Advances in Polymer Technolo-gy,2019(419) :1-20.
[2] CHAREST M,FINN R,DUBAY R.Integration of Artificial Intelligence in an Injection Molding Process for On-line Process Parameter Adjustment [C]∥2018 Annual IEEE International Systems Conference.Vancouver:IEEE,2018:1-6.
[3] 杨灿,尹 晓 红.微注塑保压时间对平面透镜相对折射率的影响[J].中国机械工程,2013 ,24(2) :158-162.
[4] ZHOU X,ZHANG Y,MAO T,et al.Monitoring and Dynamic Control of Quality Stability for Inj ection Molding Process[J].Journal of Materials Pro-cessing Technology,2017 ,249:358-366.
[5] ZARGES J C , HEIM H P , VOLKE J ,et al.Learning Quality Characteristics for Plastic Injection Molding Processes Using a Combination of Simula- ted and Measured Data[J].Journal of Manufacturing Processes,2020 ,60:134-143.
[6] 工业富联.注塑成形工艺的虚拟量测 [DB/OL].[2020-12-17] .http:∥ www.iai-lighthouse.com/ competitions/22/rankAndData.Industrial unio.Virtual Measurement of the Injection Molding Process[DB/OL].[2020-12-17].http:∥ www.iai-lighthouse. com/competitions/22/ rankAndData.
[7] 颜 诗 旋,朱 平,刘 钊.基于改进LightGBM模型的汽车故障预测方法研究[J].汽车工程 ,2020 ,42 (6) :815-819.










 玻纤含量对长玻纤...
玻纤含量对长玻纤... 钙钛矿薄膜的均匀...
钙钛矿薄膜的均匀... 用于光伏板静电除...
用于光伏板静电除... 聚砜医疗干粉吸入...
聚砜医疗干粉吸入...













