吴延凯,凌飞
河南工业职业技术学院,河南南阳473000
摘要:针对注塑机料筒温度回路非线性、大惯性、纯滞后的特点,提出一种改进粒子群算法,用其优化并行式2自由度比例积分微分(proportional integral differential,PID),并将其用于料筒温度回路。通过MATLAB仿真,验证上述方法具有响应快、调节时间短、超调量小等优点,能更好满足注塑机料筒温度的控制要求。
关键词:注塑机;料筒温度;粒子群算法;2自由度;MATLAB
引言
注塑机是一个机、电、液一体化的典型自动化控制系统,可一次成型复杂塑料产品,其适应能力强、效率高,被广泛用于国防、工业、农业等领域。因注塑技术的进步,对注塑机自动化程度要求越来越高,最突出的是料筒温度控制,温度过高、过低都会影响产品质量,因此,对料筒温度的控制就显得尤为重要[1]。对于料筒温度控制,本文提出一种并行式2自由度PID取代传统比例积分微分(proportional integral differential,PID),并提出改进粒子群优化算法(PSO)对其参数进行优化,通过仿真证明其具有优良控制效果。
1料筒温度模型建立
在注射成型中,影响塑料成型的因素很多,诸如材料结晶性、流动性、料筒温度等,而料筒温度直接关系到筒内物料均匀度,影响成品好坏。若温度过高,原料分子交融质变,间隙变大,产生发泡现象,影响注射;若温度过低,熔融不佳,螺杆间产生阻力,阻扰注射顺畅性,塑料固化在筒内产生破坏[2]。料筒加热方式是把料筒分成若干段,每段外侧放置加热器保证受热均匀,根据模具工艺需求,各段温度设置不同,可满足对熔体各段温度值的要求,生产中注塑机一般分为3段或4段加热。注塑机料筒结构如图1所示。
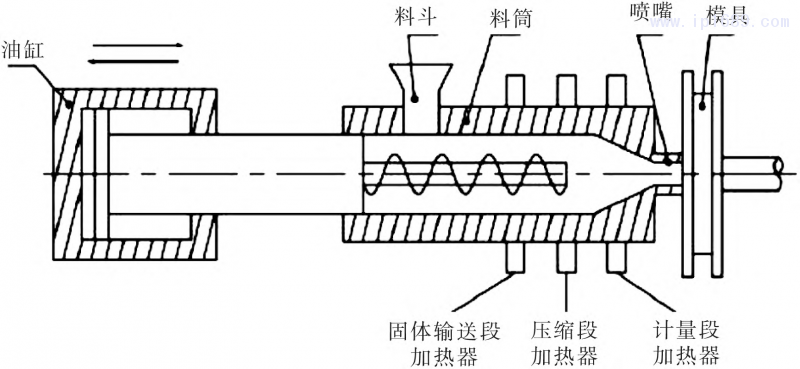
图1 注塑机料筒简图
针对料筒温度回路时间常数大、滞后时间大、耦合性强、非线性的复杂特点,可近似将其看作一阶惯性加延迟环节。对于其参数确定,可用切线法来估算模型中的增益K、时间常数T及对象纯滞后时间τ[3]。首先增益K的确定为:
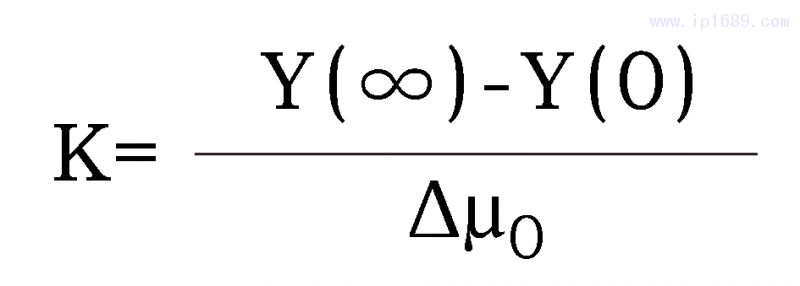
然后是时间常数T的确定,可在响应曲线上找到(t1,0.632y(∞))点,也即找到y(t1)=0.632y(∞)对应的横轴t1,则时间常数T=t1-t0。
最后是纯滞后时间τ确定,响应曲线中切线与横轴交点值即被控对象纯滞后时间τ值。
2并行式2自由度PID
在工业控制中,PID被广泛应用。若采用传统PID,参数仅有1组可调,抗扰特性、目标值追踪特性不能同时达到最优。为解决该问题,2自由度PID应运而生;实际控制中,其调节效果确实优于传统PID。具体优点为:在目标值追踪和抗扰特性上,2自由度PID可同步调整两者达到最佳状态[4]。本文在2自由度PID基础上,提出并行式2自由度PID,其结构如图2所示。
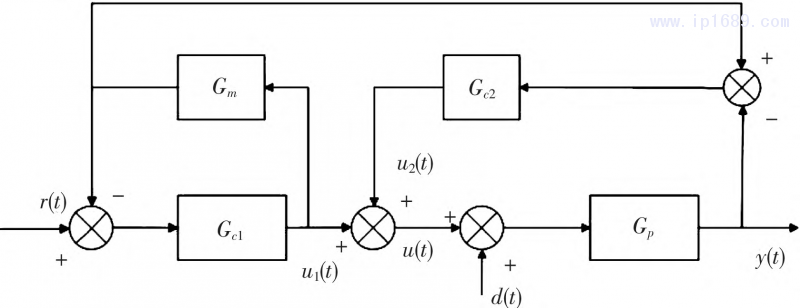
图2 并行式二自由度PID
对于PD控制器Gc1而言,系统给定值的跟踪性能受其控制,其表达式为:

对于PID控制器Gc2而言,系统抗干扰能力受其控制,其表达式为:
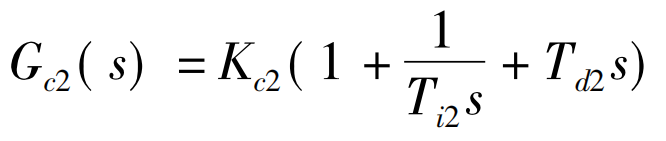
在式(2)和式(3)中,Kc1及Kc2是增益,Td1及Td2是微分常数,Ti2是积分常数。
则该2自由度的闭环输出表达式为:
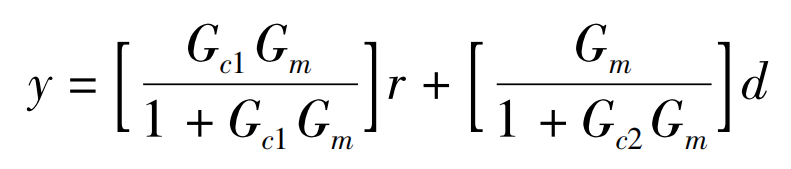
3改进PSO算法设计
遗传算法(GA)和粒子群算法都是经典群智能算法,本文在传统粒子群算法基础上,融入遗传思想,设计出一种改进PSO,该算法可弥补缺点,增强优点,相比单一算法具有更好的全局寻优能力,提高了算法性能。改进PSO引入了GA的杂交、变异算子,以扩充种群数量,防止过早收敛而陷入局部最优。为防止加入杂交、变异算子后影响算法稳定性,采用择优去劣思想,对个体适应度值从高到低排序,优先选择适应度值高的个体[5]。具体的算法原理如下。
1)将各微粒赋值随机数r1和r2,比较其值是否小于或等于杂交、变异概率来判断目前微粒是否可杂交、变异。
2)杂交单体被选中后,选择群体中随机微粒进行杂交,其子代微粒位置由双亲通过以下公式来确定。
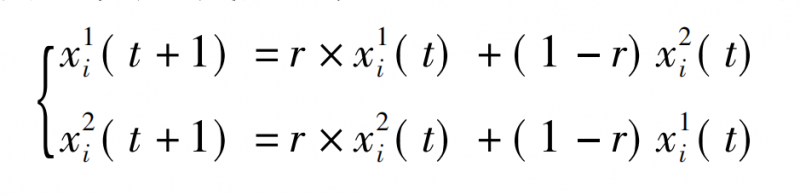
式中:xi1(t)和xi2(t)为交叉前粒子位置;xi1(t+1)和xi2(t+1)为交叉后粒子的位置;r为[0,1]的随机数。
3)变异微粒被选中后,会再次变异以产生更优秀微粒,变异的具体方式如下。
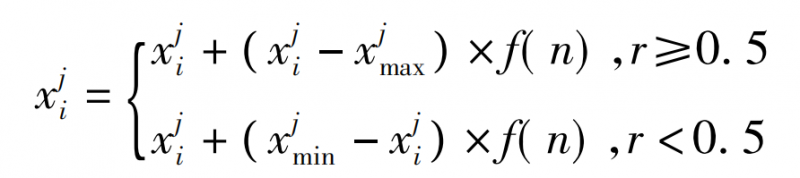
式中:xji表示第i个粒子的第j维向量;xjmin和xjmax分别为xji的上限和下限;r为随机数,n为当前迭代次数。
4)对于交叉、变异微粒,须做范围检测,对于越位微粒,采用式(7)生成新变异微粒,替换越位微粒。若微粒进化断停,过早收敛时,可越过目前位置跳入新区域继续寻优。
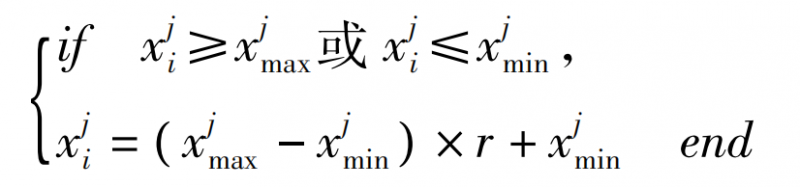
5)前面微粒在交叉、变异时,因跳跃寻优使种群复杂度得以保持,但会使种群在全局寻优中失败,故把择优去劣思想应用到算法中,以免造成优秀基因遗失。若优秀微粒数量为种群1/4,在寻优中对迭代后的种群和优秀微粒合并,按适应度值排序,去掉靠后1/4个体以保证种群数量不变,并将靠前1/4个体的速度、位置及适应度值替代旧的优良个体,以提高整体适应度值,加快算法的收敛速度。
4基于MATLAB的实例分析
为验证文中所提方法的有效性,将此方法运用到注塑机料筒温度控制回路中,通过前面的建模、辨识,确定注塑机料筒温度回路的被控对象如下。
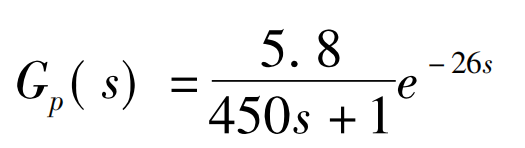
对于文中所述问题,一般取种群规模为100,可达到理想优化效果;最大迭代次数取100。在遗传算法中,交叉概率一般取0.4~0.9,文中取最大值0.9,以保证种群的多样性;变异概率取0.1;优秀个体数设置为25。
通过MATLAB仿真,得到改进PSO整定并行式2自由度PID的阶跃响应曲线、GA整定并行式2自由度PID和PSO整定并行式2自由度PID的阶跃响应曲线,如图3所示。
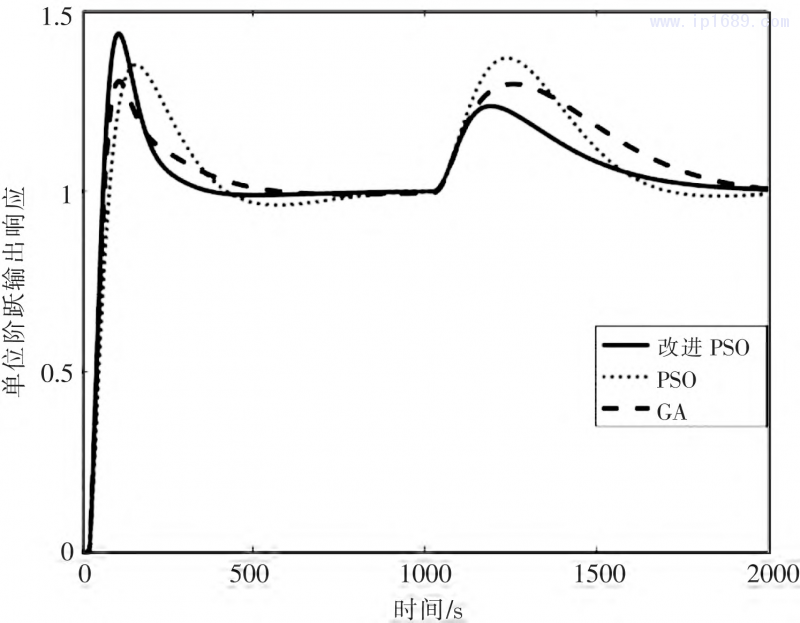
图3 控制效果对比图
运用MATLAB计算,得到目标值跟踪特性和抗扰动特性2阶段的IAE及ISE值,对应性能指标值如表1所示。

表1 不同算法控制性能对比
通过图3和表1分析知,提出的改进PSO与其他算法在优化2自由度PID参数时,均具有优良性能指标,相比其他方法有更小的超调量、调节时间、IAE及ISE。从图3也可看出,提出的方法有着更快的响应速度和较小的超调量,受到扰动后可快速稳定于终值
附近,有着更好的抗扰性能。
5结束语
本文从粒子群算法和遗传算法原理出发,发现二者具有很强互补性,提出改进PSO算法,该算法以PSO为主体,融入交叉、变异算子,可防止传统PSO早熟收敛问题。将改进PSO优化2自由度PID,并用MATLAB进行料筒温度回路仿真。试验表明:改进PSO的并行式2自由度PID在料筒温度控制中具有更优良的控制效果。
参考文献:
[1]陶西孟.注塑机温度控制系统算法研究与实现[D].绵阳:西南科技大学,2015.
[2]胡亚南,张洪兴,丰会萍.基于模糊神经网络的注塑机料筒温度控制策略[J].塑料,2019,48(4):91-95.
[3]丁锋,徐玲,刘喜梅.传递函数辨识(1):阶跃响应两点法和三点法[J].青岛科技大学学报,2018,39(1):1-14.
[4]杜祎君.串级时滞过程的分数阶二自由度控制方法研究[D].太原:太原科技大学,2021.
[5]杨智,陈颖.改进粒子群算法及其在PID整定中的应用[J].控制工程,2016,23(2):161-166.









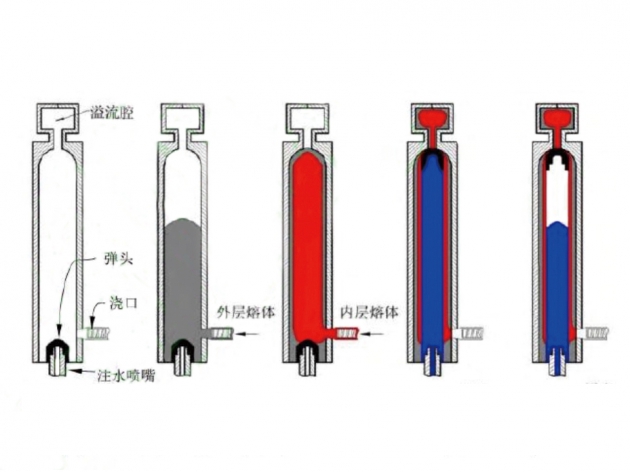 玻纤含量对长玻纤...
玻纤含量对长玻纤...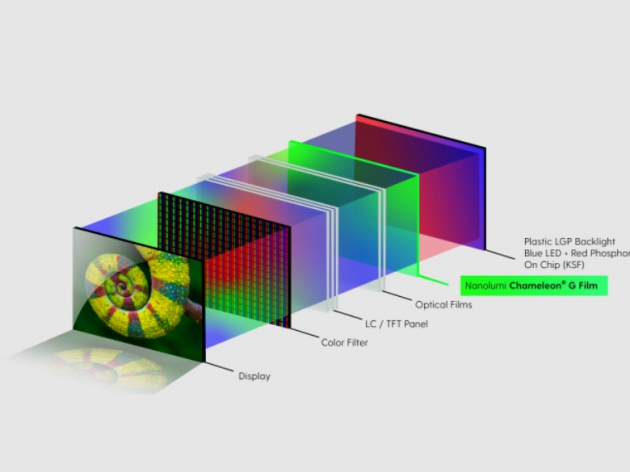 钙钛矿薄膜的均匀...
钙钛矿薄膜的均匀... 用于光伏板静电除...
用于光伏板静电除...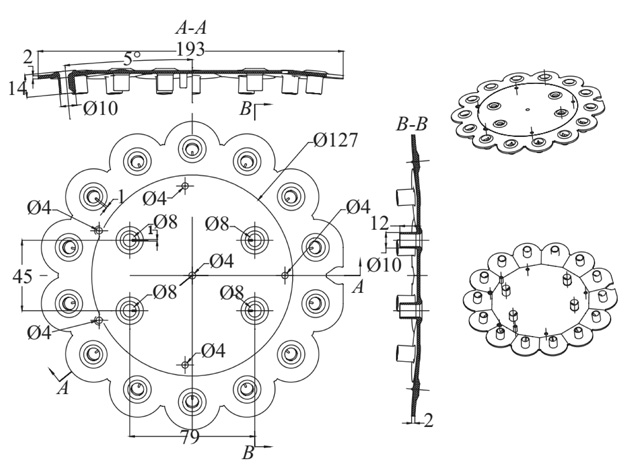 聚砜医疗干粉吸入...
聚砜医疗干粉吸入...













