郝用兴①② 张旭浩① 刘亚辉①
(①华北水利水电大学,河南 郑州450045;②河南省数字化智能装备工程研究中心,河南 郑州450064)
摘要:将壁厚减薄率和椭圆率作为管材自由弯曲成形结果的评价指标,选取弯曲模与管材间隙值、弯曲模圆角半径值、管材弯曲变形区长度、导向机构圆角半径值、导向机构与管材间隙值作为影响因子。利用数值模拟方法对管材自由弯曲成形结果的评价指标和影响因子建立样本库,并随机选取6组作为测试样本,其余的作为训练样本,结合BP神经网络和鹈鹕优化算法对预测模型进行训练,构建POA-BP神经网络预测模型对管材自由弯曲成形结果进行预测。结果表明,POA-BP预测模型的壁厚减薄率和椭圆率的最大预测误差不超过2%,故POA-BP预测模型能够有效预测管材成形结果。
关键词:管材;自由弯曲;评价指标;神经网络;预测
弯管零件能够从材料和结构满足产品轻量化、强韧化、低耗环保的需求,因此在航空、航天、船舶、汽车、医疗和能源等高技术产业得到了日益广泛的发展和应用[1]。
许多学者研究了管材弯曲过程中的起皱、管壁变薄、截面变形和回弹预测与控制等问题。田娥和刘婧瑶等[2−3]通过建立BP神经网络有效预测弯管成形的回弹量;Zhang S等[4]将管材三维回弹预测转化为二维问题,建立了平面回弹前后半径的数学关系,利用几何连续性和修正函数进行补偿,建立了可靠的三维变曲率管弯曲回弹预测数学模型;陈光耀等[5]使用RBF神经网络预测管材数控(NC)弯曲的壁厚减薄率和回弹程度,并利用支持向量机(SVM)预测管材的起皱情况,从而实现了回弹的预测和成形质量的提高;贾美慧等[6]通过粒子群算法优化的RBF神经网络实现了对管材弯曲的多目标工艺参数优化;Wu J J等[7]利用扩展卡尔曼滤波算法得出了管材成形的运动模型和观测模型,最终预测了成形轨迹并优化了加工参数,证明了加工优化方案的有效性;赵阳等[8]构建了MPSO-BP神经网络预测模型,用于小半径弯管成形结果的快速预测,并证明该模型的预测结果可靠有效。
目前针对管材自由弯曲的成形结果研究,徐振华等[9]通过解析法和有限元模拟相结合的方法预测管材自由弯曲的回弹数值,相较于传统预测方式提升了11.08%的精度;Li Y S等[10]的研究关注AL6061管材自由弯曲过程中的回弹现象,采用有限元和解析法进行研究,并通过添加中性层偏移来优化管材弯曲回弹的解析模型。另外,对管材弯曲成形结果的有效预测可以帮助相关生产部门及时评估成形品质的优劣,并为选择适当的加工参数提供有效的参考,对于推进自由弯曲成形技术的工程化具有重要意义。
本文选用外径为12mm,壁厚为1mm的TP2铜管,综合采用理论分析、数值模拟和神经网络等方法。通过数值模拟建立样本库,并基于BP神经网络建立管材自由弯曲成形结果的预测模型,使用鹈鹕优化算法优化预测模型的权值和阈值,提高预测精度,最终实现POA-BP预测模型对TP2管材三维自由弯曲成形结果的预测。
1管材三维自由弯曲
图1所示为管材三维自由弯曲的成形简图。在未成形时,管材与各个成形构件处于同一轴线上。开始成形时,管材在推进机构的作用下,沿着Z轴方向移动,导向机构在整个成形过程中对管材起着支撑的作用。球面轴承由两个伺服电机驱动,实现在XY平面内的自由移动,带动弯曲模的偏移和旋转。管材通过成形构件的共同作用,在空间范围内实现自由弯曲。
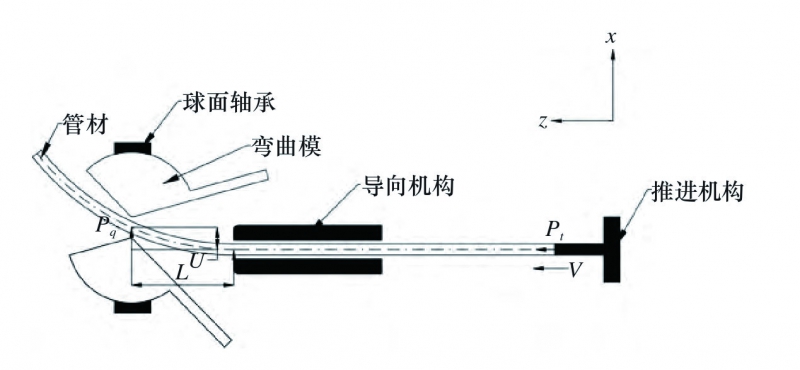
图1 管材三维自由弯曲成形简图
2管材力学性能测试与自由弯曲有限元仿真
2.1管材力学性能测试
为了准确地进行管材有限元仿真,需要获取管材的力学性能参数,管材选择ψ12mm,壁厚1mm的TP2铜管。用专用夹具塞头放置在管材两端[11],防止拉伸过程其变形。通过万能试验机对TP2铜管进行3次各向同性的拉伸试验(图2),取3次试验的平均值。经过拉伸试验后,得到的TP2铜管的材料参数,见表1。

(a)万能试验机(b)试样与塞头(c)断管
图2 拉伸试验

表1 TP2铜管材料参数
材弹性阶段的本构关系为
σ=Eε
因为管材在弯曲成形过程中存在加工硬化现象,所以使用幂指数硬化模型来描述管材的塑性变形部分。
σ=Eεn+b
其中:b为TP2铜管的初始屈服应力。
TP2管材的塑性阶段采用幂指数硬化模型,并通过拟合曲线(图3)表示。
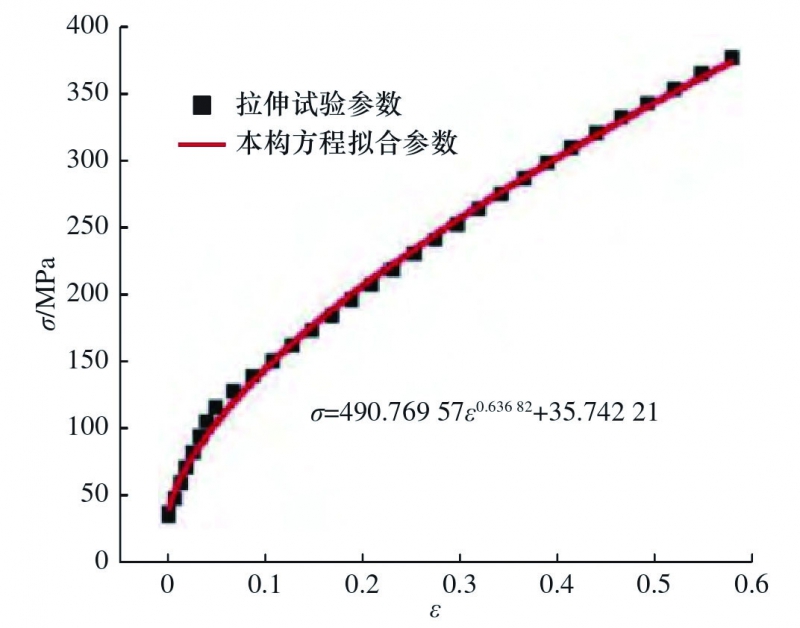

图3 σ−ε拟合曲线
2.2管材自由弯曲有限元模拟
Abaqus有限元分析软件中使用Abaqus/Explicit求解器,建立了如图4所示的三维有限元模型来模拟管材的弯曲过程。为了提高仿真效率和结果准确性,设置了质量缩放系数为25、摩擦系数为0.05,并采用通用接触来模拟管材的弯曲成形过程。该模型中,管材被定义为可变形实体,并采用S4R通用壳单元进行网格划分。球面轴承、弯曲模、导向机构和推进机构则被定义为离散刚体。弯曲模部分采用C3D8R单元进行网格划分,而导向机构等其他刚体模型则采用R3D4单元进行网格划分。各部件的网格划分如图5所示。
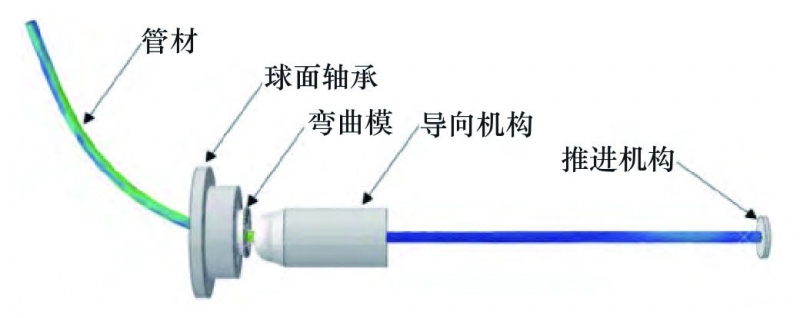
图4 管材自由弯曲有限元模型
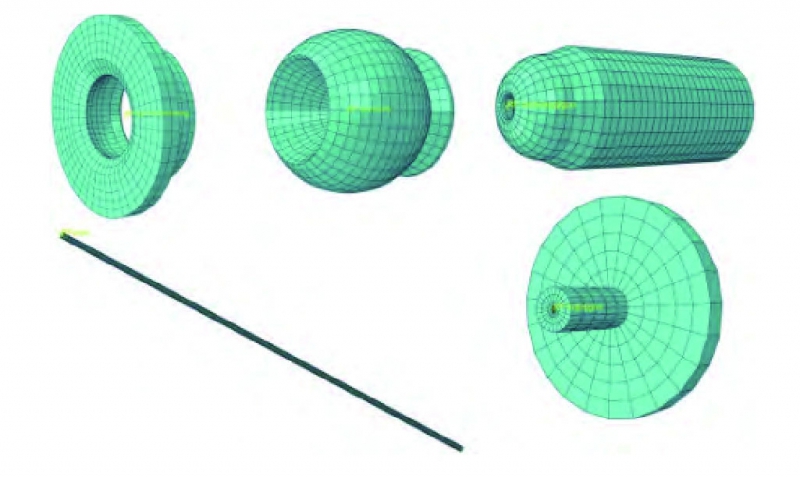

图5 各部件网格划分
管材成形结果质量的评价指标为管材壁厚减薄率δ和管材椭圆率ε为
(3)
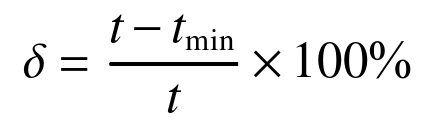
式中:t为管材的初始壁厚;tmin为管材经过弯曲后的最小壁厚。当管材的壁厚减薄率不超过10%时,即认为其质量良好。(4)
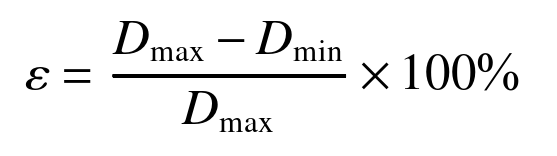
式中:Dmax表示管材经过弯曲后的最大截面直径;Dmin表示管材经过弯曲后的最小截面直径。在工业方面,铜管的椭圆率是要求不超过8%的。
3数值模拟有效性验证及训练样本和测试样本生成
3.1数值模拟有效性验证
为了确保管材自由弯曲数值模拟和实际加工相吻合,需要对管材成形数值模拟进行验证,以确保其有效性。
在有限元软件中,设置推进机构的推进速度为120mm/s、导向机构圆角半径为2mm、导向机构与管材间隙为0.3mm、弯曲模圆角半径为2mm、弯曲模与管材间隙为0.1mm、弯曲变形区长度为24mm、X轴的偏移量为0mm、6mm、0mm,Y轴偏移量为5mm、0mm、7mm,一共有3个弯曲段。
在实际加工过程中,考虑到不可控因素,设置主要参数推进机构的推进速度为120mm/s,X轴和Y轴的偏移量与数值模拟一致。
最终的仿真结果和实验结果如图6所示,两者的几何形状较为吻合。3个弯曲段的壁厚减薄率和椭圆率对比结果见表2,可以看出成形结果均符合评价指标,且这3个弯曲段的最大壁厚减薄率偏差为0.64%,最大椭圆率偏差为1.15%,管材成形质量较好,故管材成形数值模拟有效。
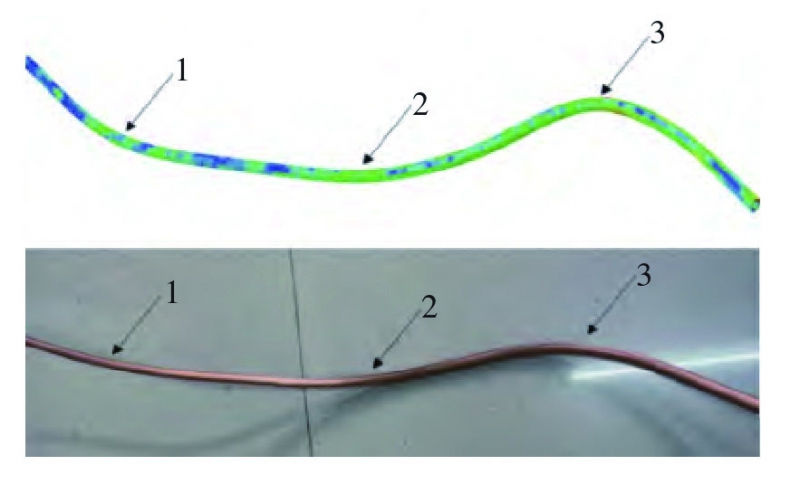
图6 模拟(上)与实验(下)弯曲成形结果对比
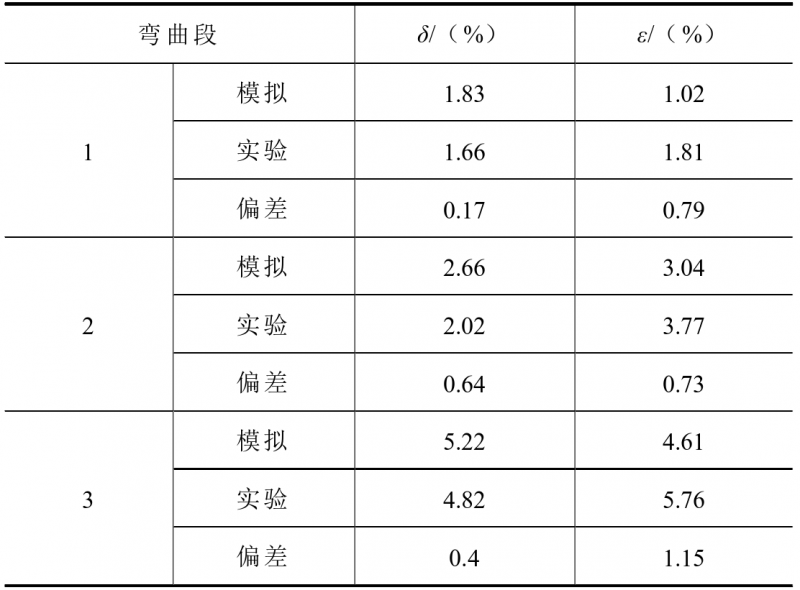
表2 模拟和实验结果对比
3.2训练和预测样本生成
相较于传统的实验加工方法,使用贴近实际加工的数值模拟可用于研究管材自由弯曲成形,同时也减少了物理实验和成本的需求。基于经过验证的有限元仿真模型和工厂加工实际情况,最终确定弯曲模与管材间隙值A1、弯曲模圆角半径值A2、管材弯曲变形区长度A3、导向机构圆角半径值A4、导向A5机构与管材间隙值作为神经网络预测模型的输入层节点。壁厚减薄率δ和椭圆率ε作为神经网络预测模型输出层节点。
根据实际加工和数值模拟分析结果,确定以下主要影响因素的取值范围为:弯曲模与管材间隙值A1为0.1~0.3mm、弯曲模圆角半径值A2为1.5~2.5mm、管材弯曲变形区长度A3为21~25mm、导向机构圆角半径值A4为1.5~2.5mm、导向机构与管材间隙值A5为0.2~0.4mm,其他参数根据实际加工情况进行设定。
根据影响因素的取值范围分散选取36组加工参数,通过数值模拟对36组加工参数进行成形,从中随机选取6组作为测试样本,剩下的30组作为训练样本。
4 POA-BP神经网络预测模型
4.1 BP神经网络及鹈鹕优化算法
4.1.1 BP神经网络
人工神经网络可处理多变量非线性优化问题并逼近任何函数。BP神经网络是一种具有多层节点的前馈神经网络,它使用误差逆向传播算法来进行训练,它具有良好的非线性函数逼近能力和时变性,常用于处理多变量非线性优化问题,网络拓扑结构包括输入层、隐含层和输出层,且三层或以上的结构可以逼近大多数的非线性函数[12],如图7所示。
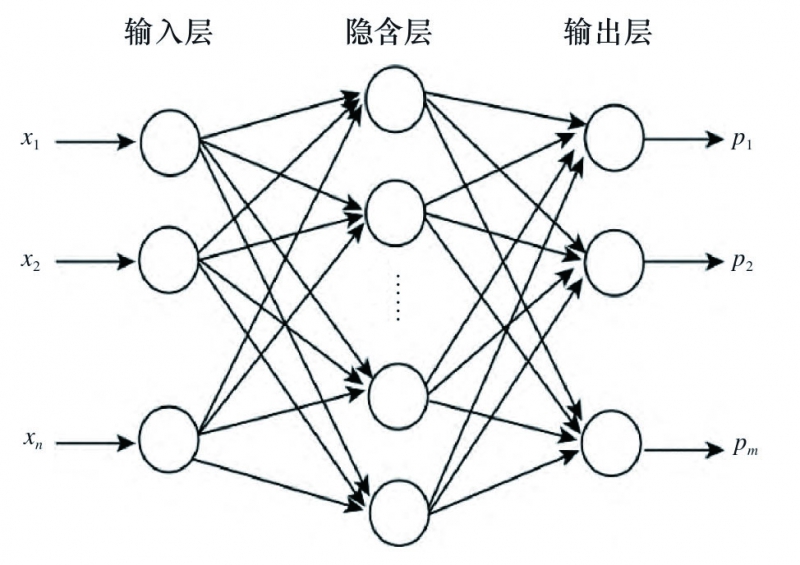
图7 BP神经网络结构
由于BP神经网络学习训练开始时,网络的结构参数是随机给定的,会出现网络的收敛速度较慢、不稳定且容易陷入局部最小值的困境,导致最大相对误差存在,从而影响网络的性能和预测准确性。
4.1.2鹈鹕优化算法
鹈鹕优化算法(pelican optimization algorithm,POA)是由Pavel Trojovský和Mohammad Dehghani在2022年提出的[13],该算法模拟了鹈鹕在狩猎过程中的自然行为,通过模拟鹈鹕鸟在觅食过程中的搜索策略和动态调整能力,来解决优化问题,如图8所示。该算法将优化问题转化为参数搜索的过程。在算法的迭代过程中,每个鹈鹕个体代表一个解,根据当前解的适应度值进行搜索和更新,通过合作与信息共享,个体之间共同寻找最优解。通过不断迭代搜索和位置调整,鹈鹕优化算法能够逐渐收敛到全局最优解,为解决实际问题提供了一种高效而灵活的优化方法。
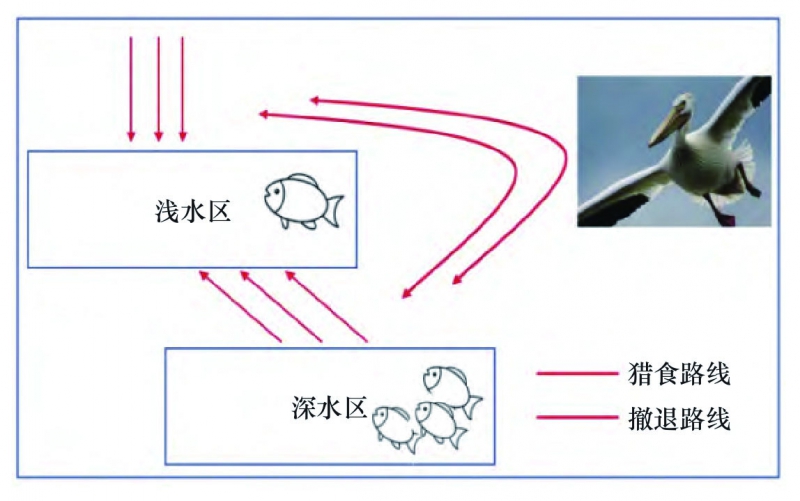
图8 鹈鹕捕猎的方式
鹕优化算法是模拟鹈鹕在攻击和捕猎猎物时的行为和策略,以更新候选解,该狩猎策略分为探索和开发两个阶段进行模拟,其数学模型如下:
(1)初始化
鹈鹕种群初始化数学描述如下:
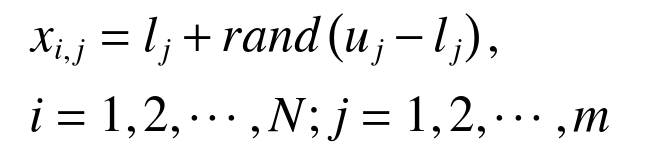 (5)
(5)式中:xi,j为第i个鹈鹕的第维的位置;N为鹈鹕的种群数量;m为求解问题的维度;rand是[0,1]范围内的随机数;uj和lj分别是求解问题的第j维的上下边界。在鹈鹕优化算法中,求解问题的目标函数可以用来计算鹈鹕的目标函数值;鹈鹕种群的目标函数值用向量(6)
式中:F为鹈鹕种群的目标函数向量;Fi为第i个鹈鹕的目标函数值;Xi表示为Xi=[ xi,1 … xi,j … xi,m ]1*m,为第i个鹈鹕的位置。
(2)逼近猎物(探索阶段)
在探索阶段,鹈鹕确定猎物位置并向其移动,通过对鹈鹕策略建模,扫描搜索空间并利用POA发现不同区域。该算法的关键是猎物位置在搜索空间中随机生成,增强了精确搜索的能力。这些概念和鹈鹕的移动策略可以用数学模型式(7)来表示。
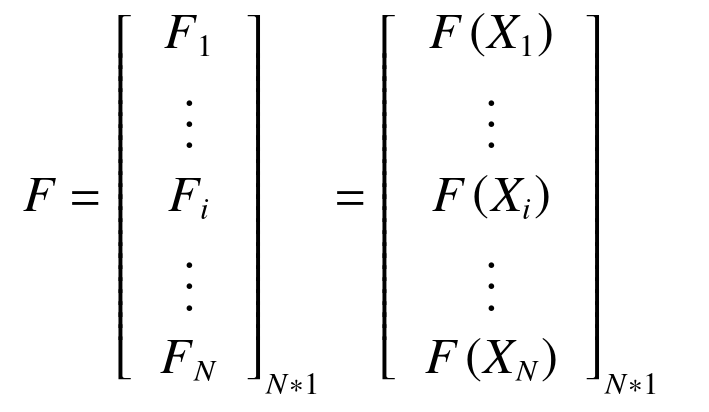 (7)
(7)式中:xp1i,j是第i个鹈鹕在第j维上基于探索阶段的新状态;Pj是猎物在第j维上的位置;Fp是猎物的目标函数值;Fi为第i个鹈鹕的目标函数值;I是为1或2的随机数。对于每次迭代和每个成员,这个参数是随机选择的。当这个参数的值等于2时,它会为一个成员带来更多的位移,这可能会将该成员带到搜索空间的新区域。因此,参数影响POA的探测能力,从而精确扫描搜索空间。
水面飞行,捕捉猎物(开发阶段)
在开发阶段,当鹈鹕达到水面时,展开翅膀驱赶猎物向上移动,并将其收集在喉袋中。这种策略使更多的猎物在攻击区域被捕获。通过对鹈鹕行为建模,POA能更好地收敛到狩猎区域的优质点,提高了本地搜索和开发能力。算法需要检查鹈鹕周围的点,以找到更好的解。鹈鹕的捕猎行为可以通过式(8)进行数学模拟。
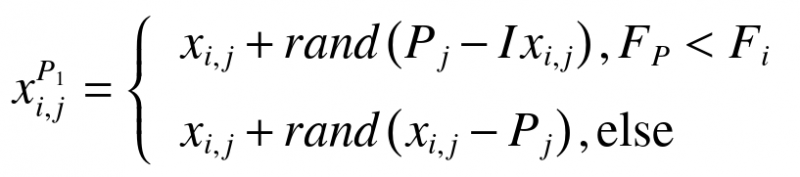 (8)
(8)式中:xP2i,j是第i个鹈鹕基于开发阶段在j维上的新状态;R(1- )为xi,j的邻域半径,R为常数0.2,t为当前迭代次数,T为最大迭代次数,系数R(1- )表示种群成员的邻域半径,用于在每个成员附近进行局部搜索,以收敛到一个更好的解。随着算法的进行,该系数逐渐减小,导致成员的邻域半径缩小,这样可以以更小、更精确的步骤扫描每个成员周围的区域,使得算法能够更接近全局最优解。
经过上述的搜索和捕获过程后,鹈鹕会再次攻击和捕猎,即进行迭代计算。不断更新最优位置,鹈鹕群需要不断地进行位置更新。根据上述得到的设计变量和目标函数值的新选择,用新得到的最优位置替换原来的最优位置,然后继续迭代计算,直到找到最优解。迭代停止并输出最终的计算结果。
4.1.3POA-BP预测模型设计
根据BP神经网络和鹈鹕优化算法的数学模型,建立管材自由弯曲成形结果预测模型的步骤如下。
(1)通过Mapminmax函数对管材自由弯曲成形结果和输入参数进行归一化处理。利用标准BP神经网络建立预测模型,并设定学习速率、学习目标、最大迭代次数、动量因子和激活函数。根据经验公式(9),选择适当数量的隐含层节点来确定BP神经网络的拓扑结构[14]。
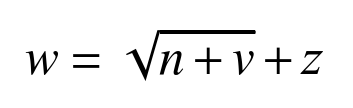 (9)
(9)式中:w为隐含层节点数;n为输入层节点数;v为输出层节点数;z为1~10的常数。
(2)初始化鹈鹕种群规模N、最大迭代次数T、搜索空间维度m等基本参数。管材自由弯曲成形结果预测模型中自变量的个数o为
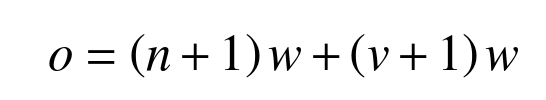 (10)
(10)(3)将BP神经网络的权重和阈值作为鹈鹕个体的参数。对于每个个体,随机初始化权重和阈值,并将其作为解的一部分。BP神经网络的均方误差(MSE)作为鹈鹕优化算法的适应度函数,表示为
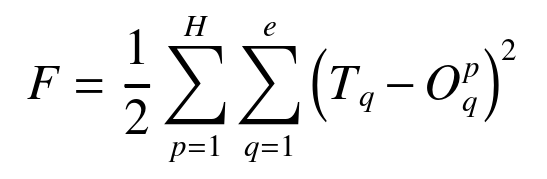 (11)
(11)式中:F为适应度函数;Tq为第q项值的期望输出,q=1,…,e,e为训练样本总数;Oq 为第q项值第p次迭代后的网络输出;H为总迭代次数,p=1,…,H。
根据上述公式计算得到最优鹈鹕个体捕捉猎物的位置,并将其存储在Xi中。
(4)根据种群的新状态和目标函数的值,将最佳的捕食位置Xi,j 方案不断地更新,得到最佳的定位方案即到达目标精度或是最大迭代次数,否则将会重复步骤(3)。
(5)将最佳结果的值赋予BP神经网络的权重和阈值,通过这些优化后的权值和阈值再次训练神经网络,直至达到目标精度或是最大迭代次数。
(6)通过步骤(5)得到的管材自由弯曲成形结果预测模型,输入新的数据即可完成成形结果的预测。
4.2管材成形结果预测模型建立
4.2.1BP神经网络预测模型
根据3.2节建立的训练和预测样本,构建3层拓扑结构的BP神经网络,输入层节点数为5,输出层节点数为2,隐含层采用tansing激活函数,输出层采用purelin激活函数,采用梯度下降动量和自适应学习率算法traingdx进行训练,目标误差为0.0001,学习率为0.05,动量因子为0.4,最大迭代次数为800。由式(10)可以得出隐含层节点数的可能取值范围为4~13,依次将不同的隐含层节点数代入训练计算得出均方误差,结果见表3,可知当隐含层节点数为13的时候,训练误差取得最小值,故5-13-2拓扑结构下的BP神经网络的预测精度最高。
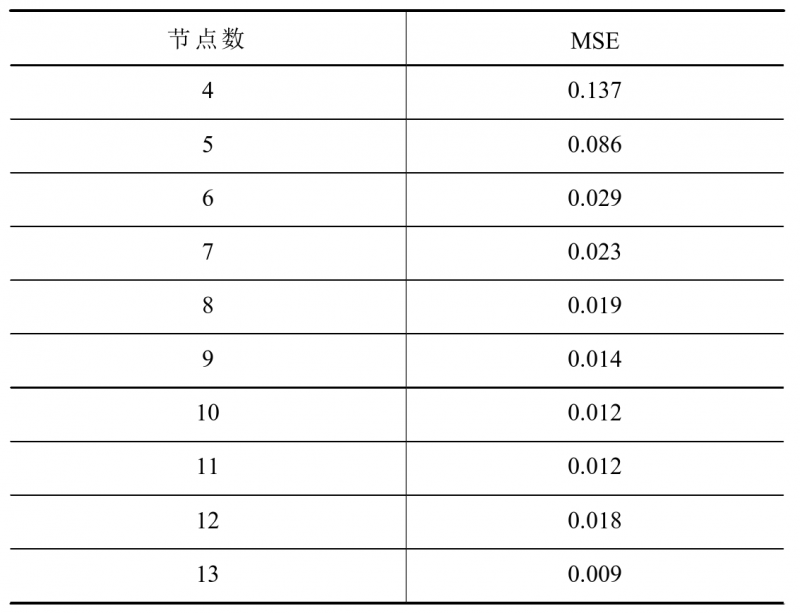
表3 不同隐含层节点数训练得到的MSE
为了深入研究具有稳定性和收敛速度快的预测模型,避免BP神经网络陷入局部最优解,需要对该BP模型进行改进。
4.2.2POA-BP神经网络预测模型
根据4.2.1小节确定的BP神经网络拓扑结构和查阅相关资料,设置鹈鹕优化算法的基本参数见表4。
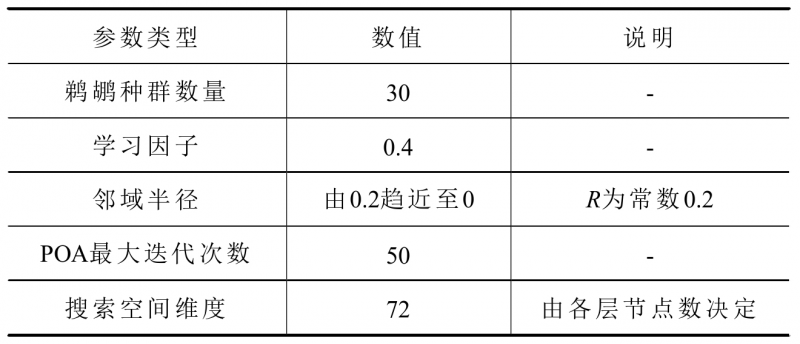
表4 鹈鹕优化算法基本参数
通过30组训练样本对POA-BP神经网络进行训练,建立POA-BP神经网络预测模型,对6组预测样本进行预测,与BP预测模型的结果进行对比,如表5和图9所示,可知POA-BP预测模型的壁厚减薄率误差It和椭圆率误差Id最大不超过2%;另外,POA-BP预测模型的决定系数高达0.99854和0.99737,不仅高于BP神经网络且更接近于1,故该神经网络模型的预测准确性和拟合性能均优于BP神经网络。
表5 BP模型、POA-BP模型的预测结果与数值模拟结果对比
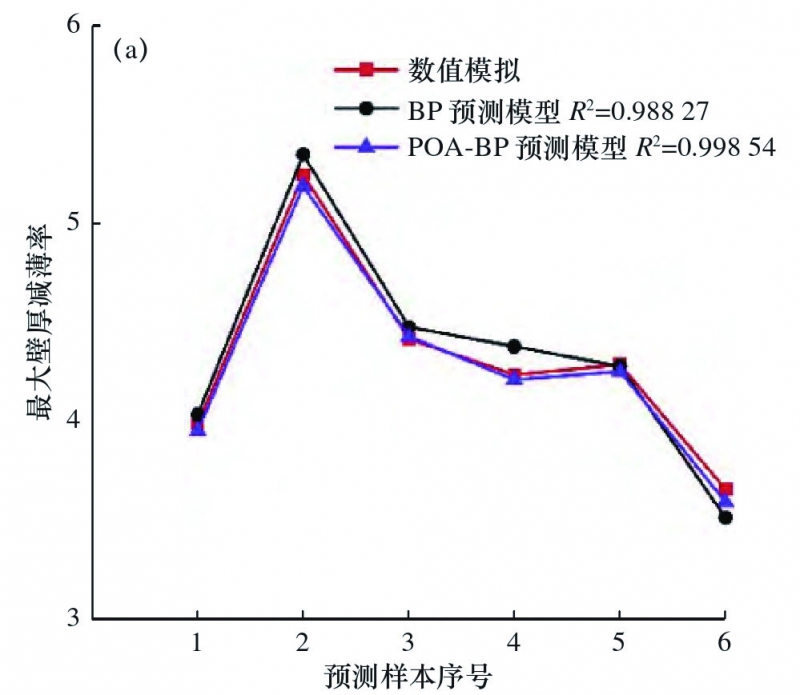
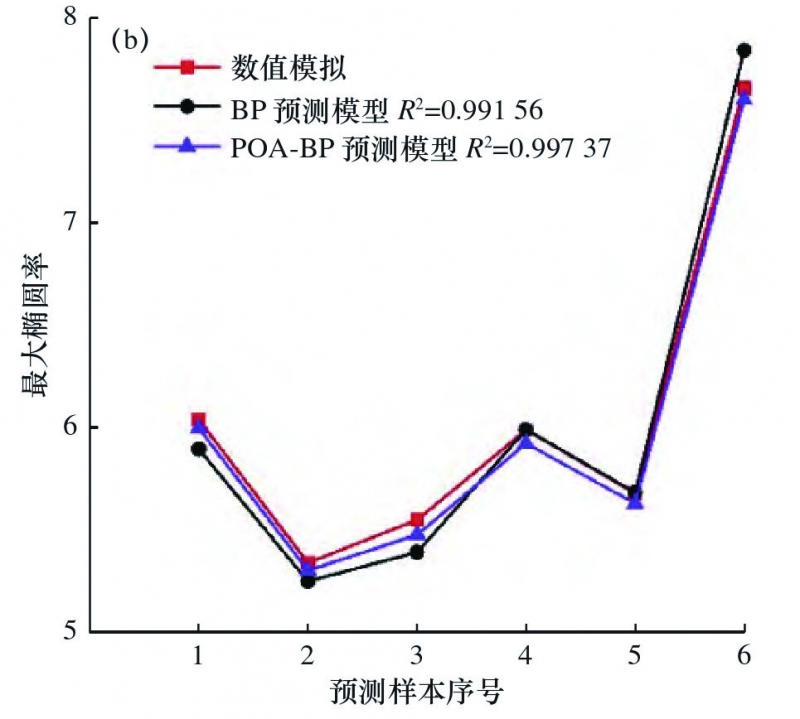
图9 数值模拟、BP预测模型、POA-BP预测模型结果对比图
4.2.3 POA-BP预测模型实验对比验证
由于本文神经网络的训练样本是基于数值模拟的,所以为了验证POA-BP预测模型在管材实际加工过程中的有效性,将随机选取的6组预测样本的加工参数通过管材三维自由弯曲成形设备进行实验,并使用手持式三维扫描仪对成形后的管材进行扫描和后处理,以测量其各参数值,如图10所示。将成形后的结果与POA-BP预测模型的结果进行对比,结果见表6。

图10 实验设备
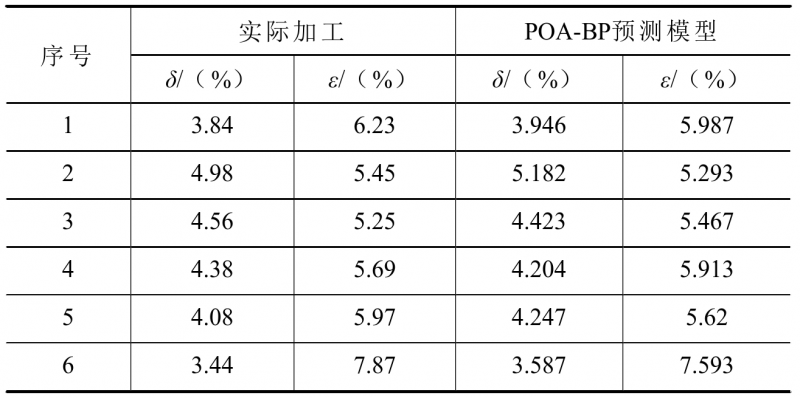
表6 实际加工与POA-BP预测模型结果对比
从表6可以看出,POA-BP模型的预测结果与实际加工的成形结果吻合度较好,说明POA-BP模型可以有效地预测实际加工的成形结果,也进一步验证了数值模拟的有效性。
5结语
(1)管材的加工参数和成形结果之间没有直接的函数关系,因此增加了准确预测管材成形结果的难度。在实际管材加工中,准确预测成形结果对生产部门至关重要。它能帮助生产部门及时评估成形结果的质量,并为选择合适的加工参数提供有价值的指导。
(2)通过鹈鹕优化算法优化后的BP神经网络模型具有更高的收敛性能、更好的拟合程度、更强的稳定性能,有效地改善了标准BP神经网络容易陷入局部最优解的问题;研究表明,POA-BP预测模型的壁厚减薄率和椭圆率的最大误差不超过2%,故采用POA-BP神经网络模型可以准确地预测管材自由弯曲的成形结果。
(3)通过对6组预测样本进行实际加工并与预测模型结果对比,验证了POA-BP预测模型在管材自由弯曲成形预测方面的实际价值。
参考文献
杨合,李恒,张志勇,等. 弯管成形理论和技术研究进展与发展趋势 (英文)[J]. Chinese Journal of Aeronautics,2012,25(1):1-12.
田娥,孙建东,刘自萍,等. 基于BP神经网络的弯管机回弹量预测[J]. 现代制造工程,2016(3):70-73.
刘婧瑶,唐承统,宁汝新. 管材数控绕弯回弹实验研究及BP网络预 测模型[J]. 塑性工程学报,2009,16(6):85-90.
Zhang S,Wu J. Springback prediction of three-dimensional variable curvature tube bending[J]. Advances in Mechanical Engineering,2016, 8(3):1687814016637327.
陈光耀,李恒,贺子芮,等. 基于机器学习的管材弯曲回弹有效预测 与补偿[J]. 中国机械工程,2020,31(22):2745-2752.
贾美慧,王成林,孙卫华. 基于神经网络和粒子群算法的管材弯曲工 艺参数优化[J]. 制造业自动化,2014,36(24):109-113.
Wu J J,Liang B,Yang J Z. Trajectory prediction of three-dimensional forming tube based on Kalman filter[J]. The International Journal of Advanced Manufacturing Technology,2022,121:5235-5254.
赵阳,刘俊,唐文勇,等. 基于MPSO-BP模型的小半径弯管成形结果 快速预测[J]. 塑性工程学报,2018,25(3):122-128.
徐振华,王华,洪荣晶,等. 基于自由弯曲技术的管材弯曲回弹预测 [J/OL]. 计算机集成制造系统:1-19[2023-04-07]. http://kns.cnki.net/kcms/ detail/11.5946.tp.20221024.0900.002.html.
Li Y S,Li A D,Yue Z M,et al. Springback prediction of AL6061 pipe in free bending process based on finite element and analytic methods[J]. The International Journal of Advanced Manufacturing Technology,2020,109: 1789-1799.
郝用兴,张少华,刘亚辉. 基于数值模拟的管材三维自由弯曲成形规 律研究[J]. 制造业自动化,2021,43(11):101-104.
Jia W K,Zhao D A,Shen T,et al. An optimized classification algorithm by BP neural network based on PLS and HCA[J]. Applied Intelligence, 2015,43:176-191.
Trojovský P,Dehghani M. Pelican optimization algorithm:A novel nature inspired algorithm for engineering applications[J]. Sensors,2022,22(3): 855.
Yong W,Feng S J. The dynamic model prediction study of the forest disease,insect pest and rat based on BP neural networks[J]. Journal of Agricultural Science,2011,4(3):291-297.









 玻纤含量对长玻纤...
玻纤含量对长玻纤... 钙钛矿薄膜的均匀...
钙钛矿薄膜的均匀... 用于光伏板静电除...
用于光伏板静电除... 聚砜医疗干粉吸入...
聚砜医疗干粉吸入...













