PE-UHMW/PE-HD熔融挤出初生丝挤出胀大现象模拟分析
付丽,薛平,刘丽超,贾明印
(北京化工大学机电工程学院,北京100029)
摘要:以熔融纺丝过程为研究对象,采用PTT本构模型,运用有限元分析方法,对高密度聚乙烯(PE-HD)改性超高分子量聚乙烯(PE-UHMW)共混物熔融法挤出初生丝的过程进行了数值模拟,对比分析了口模温度和熔体泵转速的变化对挤出过程速度场和剪切速率场分布的影响,探究了影响初生丝挤出胀大现象的因素。研究表明,随着挤出口模温度的升高,初生丝挤出胀大现象明显减弱,挤出胀大比从280℃的1.318降低到310℃的1.264。然而,随着熔体泵转速的增大,初生丝挤出胀大现象显著增强,挤出胀大比由转速为1r/min的1.258增大到5r/min的1.318。
关键词:超高分子量聚乙烯纤维;共混改性;熔融纺丝;挤出胀大;数值模拟
中图分类号:TS155.6 文献标识码:A 文章编号:1001-3539(2019)04-0053-06
超高分子量聚乙烯(PE-UHMW)纤维与碳纤维、芳纶纤维并称为世界三大高性能纤维,其优越的物理性能已使PE-UHMW纤维成为目前世界上比强度和比模量最高的纤维[1]。目前工业上主要采用凝胶纺丝法进行PE-UHMW纤维的生产,但是凝胶纺丝法工艺复杂,需要使用溶剂,成本高,易造成环境污染[2],而熔融纺丝法无需溶剂[3],工艺路线简单,成本低[4],具有很好的发展前景。
近年来,利用熔融法生产PE-UHMW纤维的研究越来越受到人们的关注。甄万清等[2]研究了纳米蒙脱土(MMT)对PE-UHMW纤维性能的影响,并从晶格变化的角度分析了纤维性能发生变化的原因;郑艳超等[5]则分析了不同聚烯烃改性材料对PE-UHMW纤维热性能、力学性能及纤维取向度等性能的影响,王非[6]、A.K.Doufas等[7]也分别做了相关研究。聚合物在熔融纺丝过程中不可避免的会出现挤出胀大以及熔体破裂现象,许多文献[8–12]利用Polyflow软件探究了工艺参数对挤出加工过程中聚合物挤出胀大现象的影响,发现利用气辅成型的方法可以有效减小挤出胀大现象;相应的挤出胀大现象对熔融纺丝过程的影响主要表现为得到的PE-UHMW初生丝的直径大于口模直径,二次拉伸之后制得的纤维尺寸也无法得到保障,这为加工生产带来不可避免的困难。然而,目前针对纺丝过程中挤出胀大现象的模拟研究[13]比较少见,尤其是PE-UHMW熔融纺丝的过程;因此笔者利用Polyflow软件进行数值模拟,对高密度聚乙烯(PE-HD)改性PE-UHMW共混物熔融纺丝过程中初生丝的挤出胀大现象进行分析研究。
1模型建立
1.1数学模型
根据PE-UHMW/PE-HD熔融纺丝过程中熔体在口模中的流动现象和特点,做出如下假设:
熔体不可压缩;流动方式为稳定的层流;忽略重力和惯性力的影响;熔体为黏弹性流体且等温流动。
连续性方程:
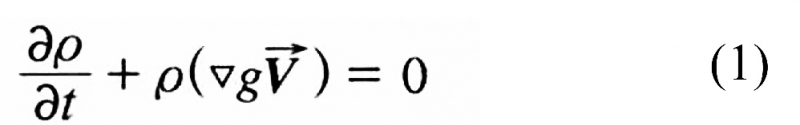
式中:
——速度矢量;
ρ——密度;
V——哈密尔顿算子。
动量方程:
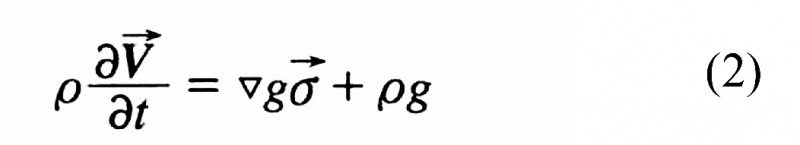
式中:
——应力矢量;
g——重力加速度。
1.2材料模型
材料模型主要反映的是共混物料流动过程中应力和应变之间的关系。模拟过程中只有真实的反应这两者之间的关系,才能得到相对准确的模拟结果。此处采用PTT微分黏弹模型,因为该模型能够定量地描述聚合物的剪切黏度和法向应力差,对于粘弹性流体的流动来说,额外应力张量分为黏弹性张量T1和牛顿分量T2,即T=T1+T2,其中牛顿分量T2=2η0D,其粘弹性分量T1计算方法如式(3)所示:
式中:η0——零切黏度;
η1——模型指定黏度系数;
λ——松弛时间;
tr——张量微量;
η2——牛顿分量黏度系数;
D——变形速率张量;
ξ——与剪切有关的材料参数;
ε——与拉伸黏度有关的材料参数;
V——下随体时间导数;
Δ——上随体时间导数。
1.3几何模型
根据课题组之前的研究表明[7],PE-UHMW/PE-HD共混物熔融纺丝过程中圆柱形挤出口模长径比L/D为5,口模直径D为0.6mm,口模收敛角为70°时,初生丝具有较好的挤出稳定性,同时模具也容易被清理,因此选用该结构的喷丝板,其物理模型如图1所示。
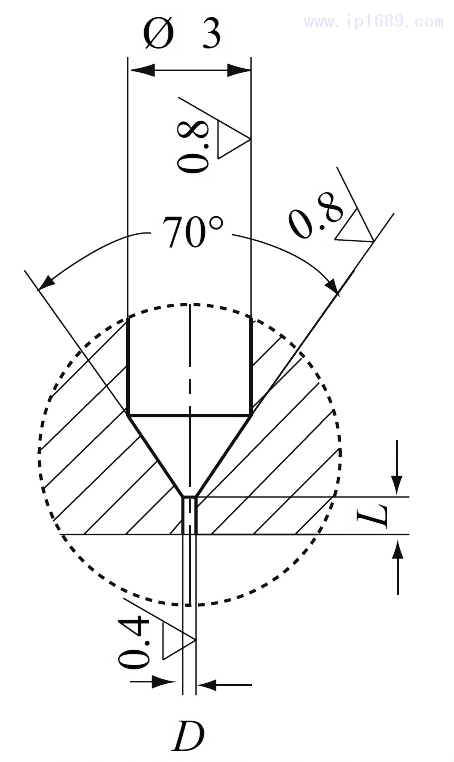
图1挤出口模物理模型
2数值模拟
2.1三维模型建立
根据熔融纺丝挤出口模的物理模型,利用SolidWorks软件建立三维模型,挤出口模三维模型示意图如图2所示。由于口模具有很好的对称性,为减减少计算时间,方便分析,只对挤出口模的四分之一进行数值模拟。
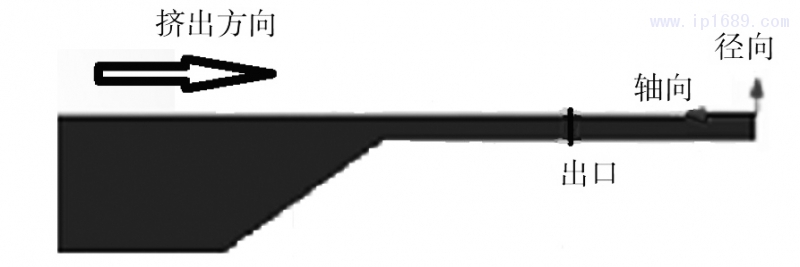
图2挤出口模三维模型
2.2网格划分
将三维模型导入GAMBIT软件,利用GAMBIT软件对流道中的物料进行网格划分,挤出物网格划分的结果如图3所示。
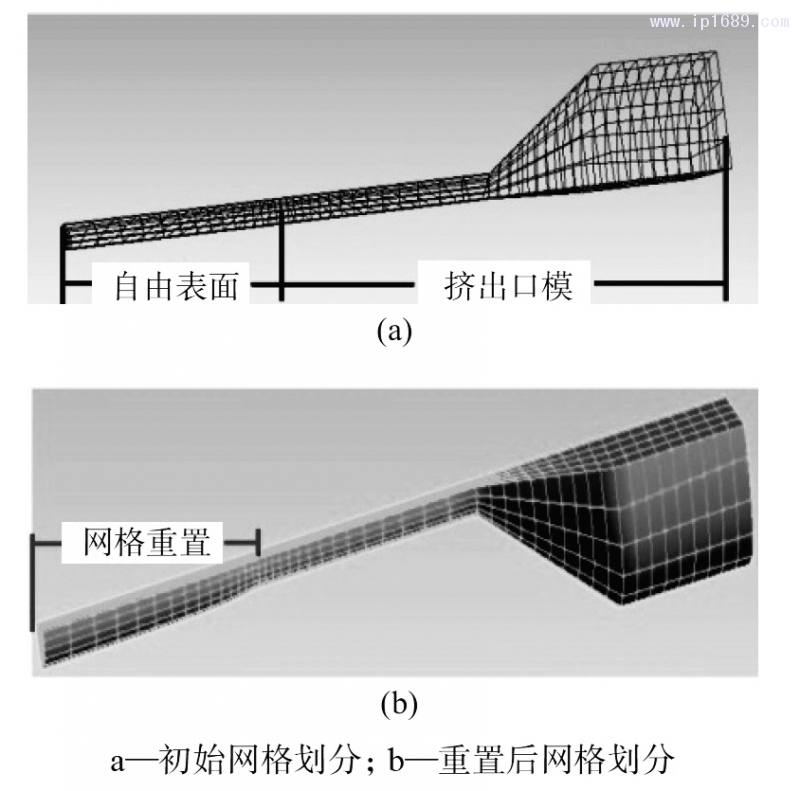
图3挤出物网格划分
图3a显示是初始网格划分,共划分单元3096个,节点4420个,边界6个,邻域2个。挤出过程中,物料在挤出口模后,会发生挤出胀大现象,因此模拟过程中会发生网格重置现象,如图3b所示。
2.3材料参数和工艺参数
笔者主要研究挤出口模温度和熔体泵转速对PE-UHMW/PE-HD共混物熔融纺丝挤出胀大现象的影响,而实验过程中挤出口模的温度一般设定在280~310℃[15],熔体泵转速设定在1~5r/min,因此模拟过程中温度和转速的变化也分别设定在这个范围内。
利用哈克旋转流变仪测定不同温度下PE-UHMW/PE-HD共混物的各项性能,发现其零切黏
度、稳定剪切黏性流动的无量纲材料参数、稳态拉伸黏性流动的无量纲材料参数及纯黏性部分与总黏度的比值几乎不发生变化,分别为9000Pa·s,0.75,0.63,1/9;松弛时间随着温度的升高而减小,在不同温度下,分别为0.0155,0.0112,0.0091,0.0062,0.0059,0.0055,0.0034s(280~310℃,每5℃测一次)。
2.4边界条件
口模入口处:分别设定入口体积流率为5×10–8m3/s(1r/min),1.0×10–7m3/s(2r/min),1.5×10–7m3/s(3r/min),2.0×10–7m3/s(4r/min),2.5×10–7m3/s(5r/min)。
自由表面末端处:fn=fs=0;
口模内壁面:vn=vs=0;
初生丝表面:自由表面;
XY面和YZ面:对称面。
vn表示法向速度,vs表示切向速度;
fn表示法向力,fs表示切向力。
2.5结果处理
综合上述的物料参数、本构模型及边界条件的设置,运用Polyflow进行数值计算,并利用该软件的CFD-post功能进行结果处理,输出挤出口模处的速度分布云图和剪切速率分布云图,分析挤出口模处的速度和剪切速率的变化趋势,计算挤出胀大比等数据。
3结果分析
3.1速度场分析
共混物挤出口模的过程中,受到壁面无滑移条件的影响,口模中熔体流动速率的梯度分布是发生挤出胀大的重要因素,尤其是挤出口模径向方向上的速度梯度。
图4是初生丝速度分布图。口模内物料的轴向流动在失去壁面的束缚后,在口模外表现为轴向流动和径向流动的叠加,从而产生明显的挤出胀大现象(如图4a所示)。不同加工温度、不同熔体泵转速下挤出口模的轴向速度和径向速度分布变化情况如图4b~图4e所示。由图4b和图4d可以看出,不同温度和转速下,物料在流出挤出口模的瞬间,轴向方向的速度急剧降低,根据公式(2)中的动量方程可以分析得出,此时物料的流动由口模内的轴向流动转变为径向流动和轴向流动的叠加,如图4c和图4e所示,而且挤出口模温度和计量泵转速越高径向速度越大,这主要是因为物料在口模中流动发生较高程度的取向,但是在离开口模后,失去口模的束缚,分子链发生解取向导致的弹性恢复现象;在离开口模一段时间后,分子链的解取向过程逐渐结束,径向速度逐渐减小,几乎变为0,此时物料的流动主要表现为轴向流动,即图4b和图4d中距口模出口0.5mm的位置,轴向速度急剧增大的现象,相应地,当径向流动停止后挤出物的直径就不再发生变化。
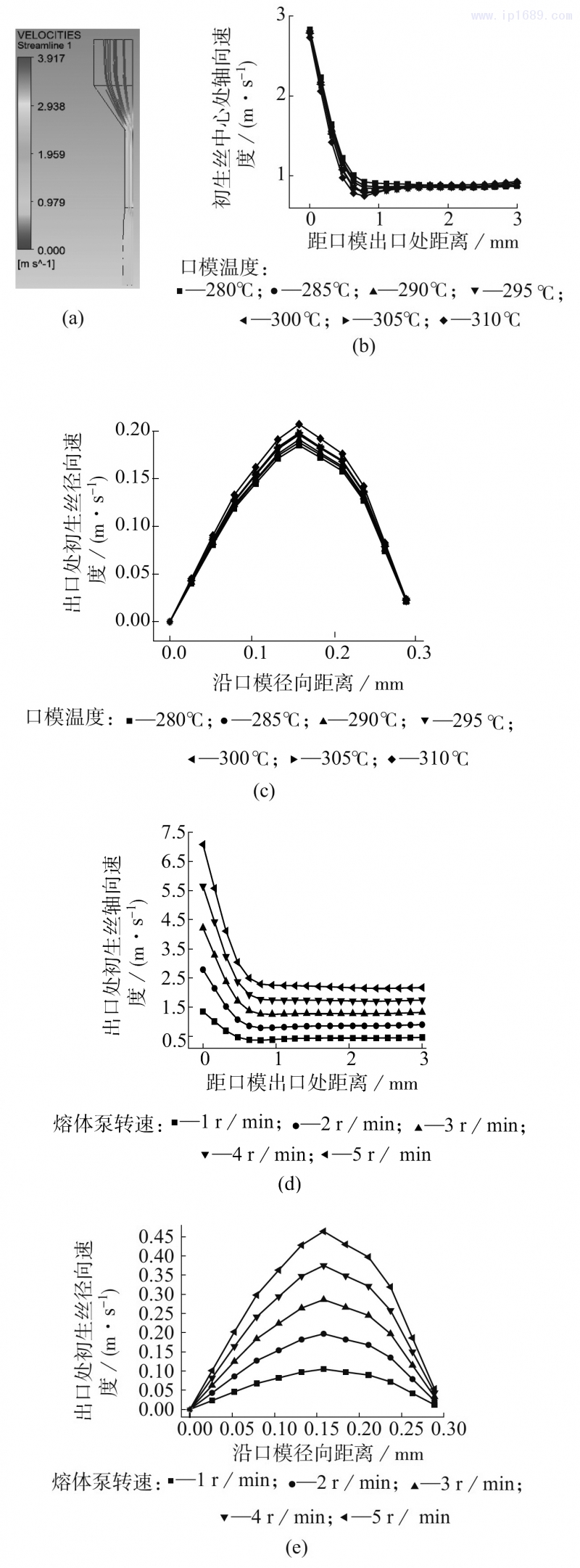
a—初生丝挤出口模过程中速度分布流线图;
b—熔体泵转速为2r/min时,不同口模温度下初生丝中心处的轴向
速度分布;c—熔体泵转速为2r/min时,不同口模温度下出口处初
生丝径向速度分布;d—口模温度为300℃时,不同熔体泵转速下初生
丝中心处的轴向速度分布;e—口模温度为300℃时,不同熔体泵转速
下出口处初生丝径向速度分布
图4初生丝速度分布图
3.2剪切速率场分析
剪切速率的分布对分子链的取向和解取向过程有很大的影响。图5为初生丝剪切速率分布图。由图5a可见,受到口模壁面的作用,径向方向上的速度梯度较大,因此近壁面处物料受到的剪切速率最大,而在口模中心处,径向方向上速度梯度小,口模中心处的剪切速率也减小。共混物料流出挤出口模后,物料的流动由口模内的轴向流动变为口模外的轴向流动和径向流动的叠加,因此在挤出口模后,由于没有了壁面的作用,初生丝外壁面处的剪切速率最小,但是受到径向流动的影响,剪切速率由中心沿径向方向逐渐减小,直至径向方向上的速度变为0,剪切速率变成均匀分布。由图5b和图5c可看出,熔体泵的转速不变时,随着温度的升高,最大剪切速率值沿径向方向几乎没有发生变化,而在温度不变时,随着熔体泵转速的增大,剪切速率在径向方向上的分布成比例的增大,说明物料挤出口模的过程中速度梯度是影响剪切速率的主要因素。图5c可以看出,熔体泵转速越大,口模内最大剪切速率和最小剪切速率的差值越大,说明在离开口模后,没有了壁面的约束,初生丝外壁面处剪切速率发生突变,但是中心处的剪切速率受到熔体的黏性作用,无法发生突变,因此剪切速率由梯度分布变为均匀分布的时间更长,挤出胀大现象更明显。
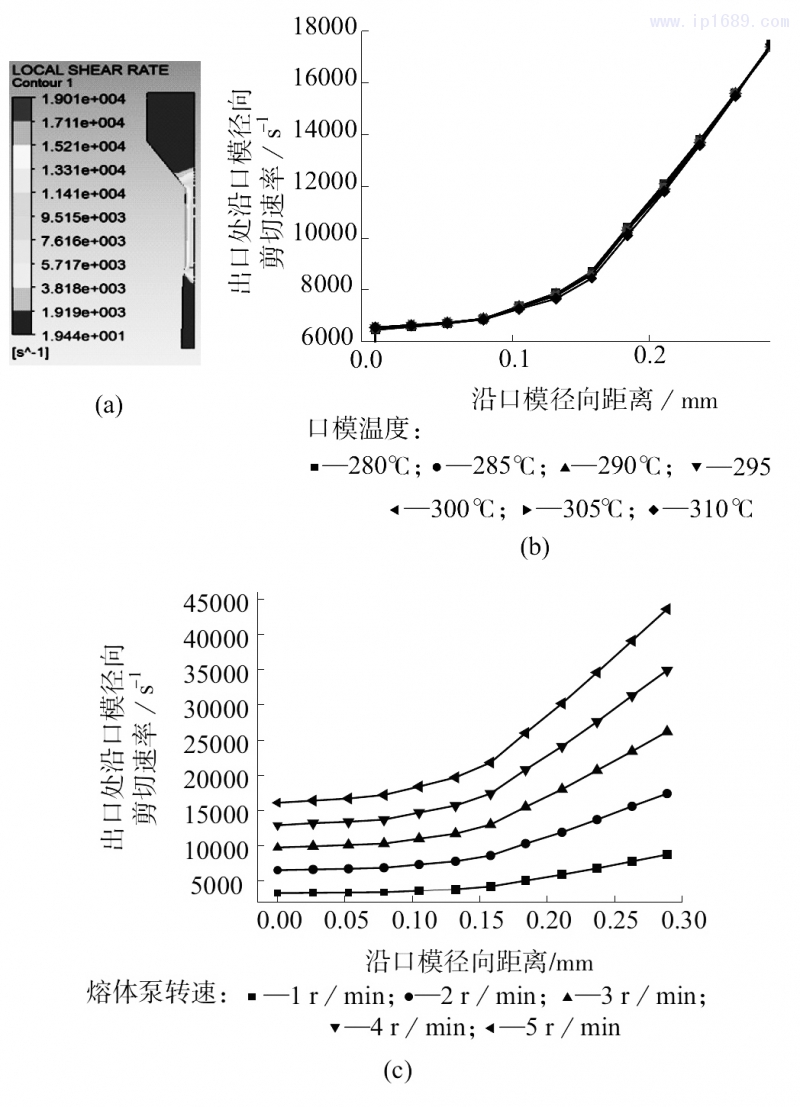
a—初生丝挤出口模过程中剪切速率分布云图;b—2r/min时,不同
口模温度下出口处初生丝径向剪切速率分布;c—300℃时,不同熔体
泵转速下出口处初生丝径向剪切速率分布
图5初生丝剪切速率分布图
3.3挤出胀大现象分析
挤出胀大现象一般利用挤出胀大比来表征,此处将流出挤出口模后的初生丝直径和口模截面直径之比定义为挤出胀大比,其计算方法如式(4)所示。
式中:B——挤出胀大比;
D——初生丝截面直径;
D0——挤出口模截面直径。
纺丝过程中的挤出胀大现象,直观地表现为初生丝的直径大于挤出口模的直径,但是受到口模温度、熔体泵转速等工艺参数的影响,挤出胀大率会发生较大的变化。图6为常见挤出胀大现象示意图(1/4部分),其中内圈表示挤出口模,外圈表示初生丝。
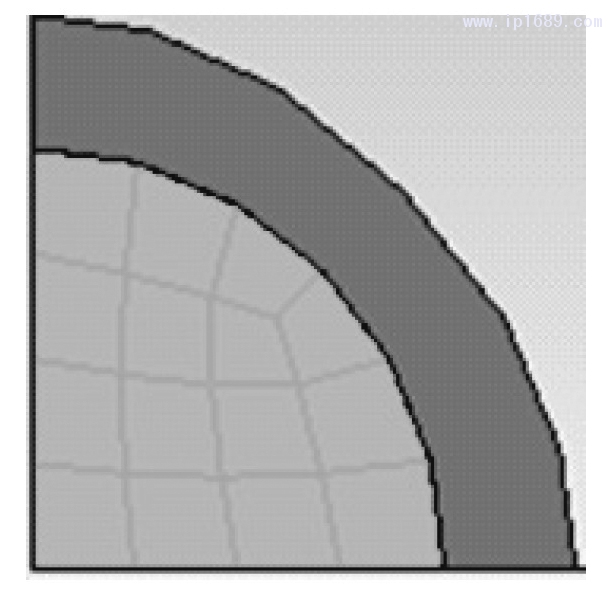
图6纺丝过程中挤出胀大现象示意图
(1)口模温度对挤出胀大比的影响。
纺丝过程中,挤出口模的温度是重要的工艺参数,直接影响了物料的塑化状况及分子链的取向及解取向状况。图7为初生丝挤出胀大比随温度变化。由图7可见,随着温度的升高,初生丝的挤出胀大比呈下降趋势,由280℃时的1.318降低到310℃的1.264,而且其减小趋势与物料松弛时间的减小趋势几乎相当。这主要是因为在固定熔体泵转速的情况下,物料流经挤出口模的时间是相同的,而松弛时间的减小会使口模中取向的分子链更快地解取向,即在口模内已经发生解取向;此时,聚合物分子链的运动能力明显增大,熔体在流动过程中储存的形变能明显减小,弹性特性减弱,因此温度越高,离开挤出口模的初生丝取向度越低,初生丝因解取向而发生弹性恢复的可能性越小,挤出胀大现象越不明显,挤出胀大比越小。
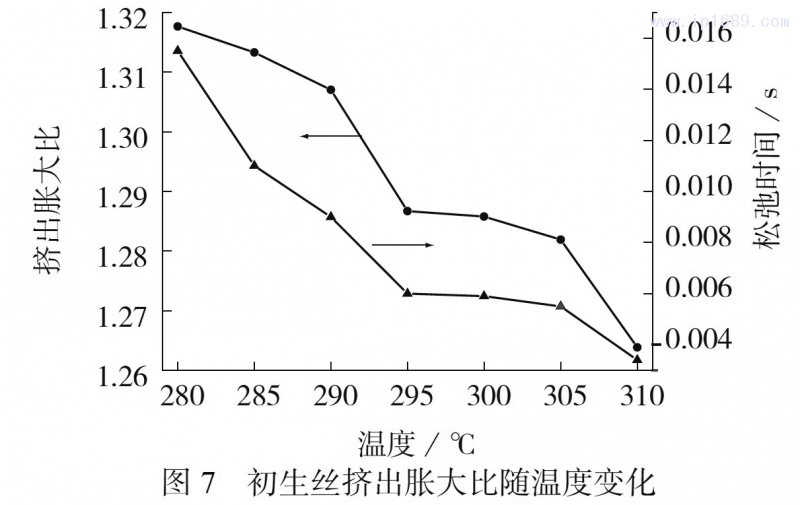
图7初生丝挤出胀大比随温度变化
(2)熔体泵转速对挤出胀大比的影响。
熔体泵转速对初生丝挤出胀大的影响主要表现为:熔体泵转速的增加在一定程度上增大了口模径向方向的速度梯度,从而增大了分子链的取向度;熔体泵转速的增大使物料在挤出口模中的停留时间减小,使分子链在挤出口模内部发生解取向的可能性减小。
图8为初生丝挤出胀大比随熔体泵转速变化。由图8可见,随着熔体泵转速的增加,挤出胀大比逐渐增大,由转速为1r/min的1.258增大到5r/min的1.318。挤出胀大比随熔体泵转速的增大而增大,这是因为:一方面,熔体泵转速的增大使挤出口模径向方向的速度梯度增大,如图4e所示,微观上,径向速度梯度的分布增大了大分子链之间的内摩擦,内摩擦力使聚合物大分子链沿轴向方向取向,而且一定程度上速度梯度越大,内摩擦越大,分子链取向越明显,离开口模后的回弹现象越严重,挤出胀大现象越明显;宏观上,径向速度梯度的分布使口模内部物料受到的剪切速率增大,导致物料内部的法向应力差增大,挤出胀大比也增大。另一方面,熔体泵转速的增大使物料在口模的停留时间减小,但是相同时间聚合物熔体的松弛时间是不变的,因此停留时间的减小使取向的分子链在口模中发生解取向的可能性减小,也就是说,在一定范围内,熔体泵转速越大,聚合物熔体在口模内的停留时间越短,聚合物大分子链在口模内的解取向程度越小,挤出口模后初生丝的回弹能力越强,挤出胀大现象越明显,挤出胀大比越高。可以看出,速度梯度分布和停留时间对于PE-UHMW/PE-HD共混物熔融纺丝过程中的挤出胀大现象具有双重作用。
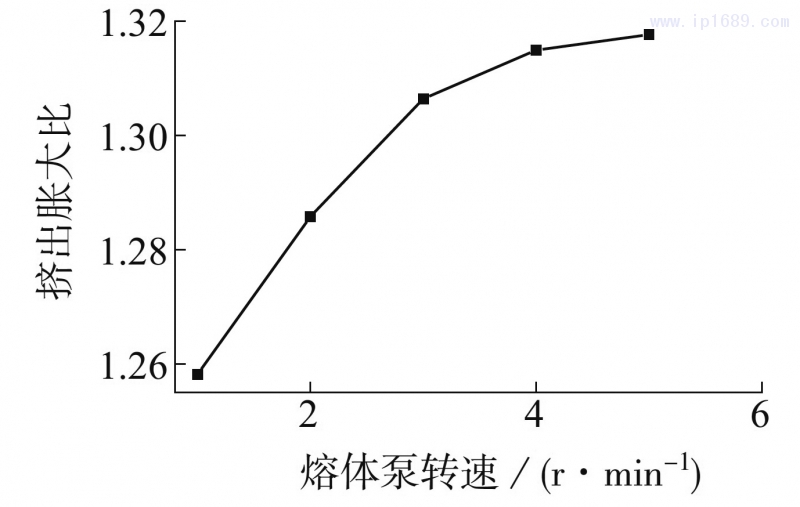
图8初生丝挤出胀大比随熔体泵转速变化
4结论
通过数值模拟分析PE-UHMW/PE-HD共混物纺丝过程中初生丝在不同温度和不同熔体泵转速下的物料流动状况,可得到以下结论:
(1)在一定的温度范围内,初生丝的挤出胀大比随挤出口模温度的升高而降低,由1.318(280℃)减小到1.264(310℃);
(2)在一定的熔体泵转速内,初生丝的挤出胀大比随熔体泵转速的增加而增大,由1.258(1r/min)增大到1.318(5r/min)。
参考文献:
[1] 陈利民.超高分子量聚乙烯纤维在防弹材料上的应用[J].工程塑料应用,1995,23(6):31–34.
[2] 甄万清,王庆昭,吴进喜,等.熔融纺丝法制备UHMWPE/MMT复合纤维的研究[J].合成纤维,2011,40(3):5–9.
[3] Liang J Z. Effects of extrusion conditions on die-swell behavior of polypropylene/diatomite composite melts[J]. Polymer Testing,2008,27(8):936–940.
[4] 黄伟,王晓春,杨中开,等.UHMWPE/聚烯烃共混物的性能及其熔融纺丝研究[J].合成纤维工业,2015,38(6):43–48.
[5] 郑艳超,杨中开,王晓春,等.熔纺PE-UHMW/聚烯烃共混体系及其纤维结构性能研究[J].北京服装学院学报:自然科学版,2017(1):8–17.
[6] 王非.高密度聚乙烯改性超高分子量聚乙烯熔融纺丝的研究[D].北京:北京化工大学,2017.
[7] Doufas A K,Mchugh A J,Miller C. Simulation of melt spinning including flow-induced crystallization:Part I.Model development and predictions[J]. Journal of Non-Newtonian Fluid Mechanics,2000,92(1):27–66.
[8] 邓小珍,柳和生,黄益宾,等.非等温气辅共挤出胀大的三维粘弹数值模拟[J].高分子材料科学与工程,2013,29(3):169–172.
[9] 李萍.聚合物气体辅助挤出成型工艺及数值模拟[D].哈尔滨:哈尔滨理工大学,2010.
[10] 徐妍清.聚合物圆管气辅挤出数值模拟与口模设计[D].南昌:南昌大学2015.
[11] 何建涛.塑料异型材气辅共挤数值模拟与实验研究[D].南昌:南昌大学,2014.
[12] 曹义.熔融纺丝组件熔体流动数值分析及其结构设计优化研究[D].上海:东华大学,2006.
[13] Wang Fei,Liu Lichao,Xu Ping,et al. Crystal structure evolution of UHMWPE /HDPE blend fibers prepared by melt spinning[J].Polymers,2017,9(12):doi.org/10.3390/polym9030096.









 玻纤含量对长玻纤...
玻纤含量对长玻纤... 钙钛矿薄膜的均匀...
钙钛矿薄膜的均匀... 用于光伏板静电除...
用于光伏板静电除... 聚砜医疗干粉吸入...
聚砜医疗干粉吸入...













