胡玉玲,刘淑梅,廖秋慧,高 冲
( 上海工程技术大学,上海 201620)
摘要:通过三因素三水平正交试验的设计以及型坯12段非等厚度优化的方法,得到最优工艺参数组合,最终实现吹塑件壁厚合格且均匀性明显提高。采用Workbench-Polyflow分析软件进行型吹胀过程的数值模拟[1]。完成9组方案的模拟后,选取12个特征点的厚度值作参考代替整体厚度均匀性,经方差分析得出:工艺参数最优解为吹胀压力A(0.456MPa)、吹胀时间B(1.210s)、模具运动速度C(0.878m/s)。影响权重大小为B<A<C。为了得到符合实际生产标准的制件,在最优工艺参数的基础上,进行型坯的非等厚度优化,结果方差降低45%,壁厚均匀性显著提高,壁厚平均值为0.773mm,最低厚度0.556mm,经生产验证,产品厚度合格。
关键词:挤出吹塑;正交试验;数值模拟;非等厚度型坯;工艺优化
0 引言
挤出吹塑过程是1个大变形、大应变的过程,包括型坯成型、型坯吹胀和制品冷3个阶段[2]。当型坯与模具型腔接触时,变化机理极其复杂,导致壁厚不均匀的直接原因是型坯吹胀过程中各部位的形变不一致[3]。1 L墨水瓶是常见的日用品,采用挤出吹塑成型,要求壁厚0.5~1mm。但生产中普遍存在厚度不均的问题,厚度不均将会造成材料的收缩不一致,厚壁位置会在表面出现缩水,凹坑等问题,影响外观,而且厚壁与薄壁转接处会产生内应力,影响产品的强度[4]。文章从成型工艺条件的角度出发,探讨了其对制品厚度的影响,改善了壁厚不均的情况。
1 三维模型与网格划分的建立
假设熔体是不可压缩、等温流动且连续的,其流动遵循质量守恒定律、动量定律、能量守恒定律[5]。常用的1 L墨水瓶几何模型如图1所示,高235 mm,瓶口直径23 mm,最大宽度和长度80mm,假设型坯直径45 mm,吹胀比为1.78,模具到型坯中心距离为50 mm。假设其为等温模具,并对型坯和模具进行网格划分[6],如图2所示。
2 正交试验设计及结果
2.1 正交试验设计
吹胀压力可以使型坯变形紧贴模具型腔壁,并对产品进行保压、冷却[7]。合理的压力范围将得到合格的产品。研究压力大小,吹压时间和模具运动速度三素对成型制件壁厚的影响。正交试验方案设计如下:(1)由于实验条件不易精确控制,并能大致获取工艺参数的适当取值范围2个原因[8],将吹塑压力大小、吹胀时间和模具运动速度三因素分别设计3个水平。各因素水平如表1所示。(2)试验涉及三因素三水平,不考虑交互作用,采用L9 (33)正交表,正交试验方案如表2所示。
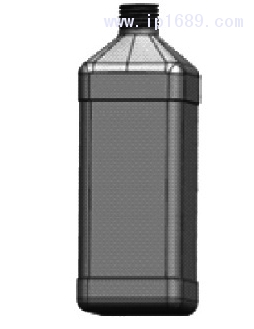

图 1 三维模型图 图2 型坯与模具网格
表 1 正交试验设计
2.2 有限元数值模拟及结果
2. 2. 1 边界条件设定
在workbench模块中,建立2D-shell Geometry 瞬态分析任务,设置流动边界条件[9]。分析任务包含定义模具和子任务型坯。其中,定义模具包含定义模具区域、接触条件及模具运动参数,而子任务包含定义型坯区域、流动条件、材料属性、初始厚度、吹胀压力等。9组正交试验方案中,型坯初始厚度设为0.0018 m,重力为-9.81m/s,产品材料HDPE,密度为900g /cm3,黏度为10 000Pa·s,考虑惯性因素。
模具的运动速度是1个随时间变化的函数,因此,采用渐进函数f(t)—斜坡函数实现模具运动[10],斜坡函数曲线如图3所示。以方案A1B1C1为例,斜坡函数的参数如图3、4 所示。
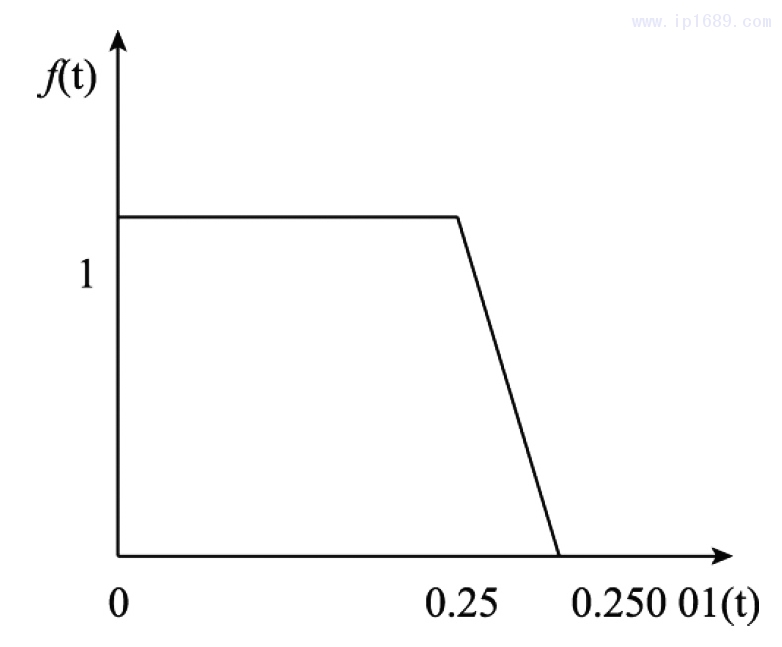
图 3 模具运动斜坡函数
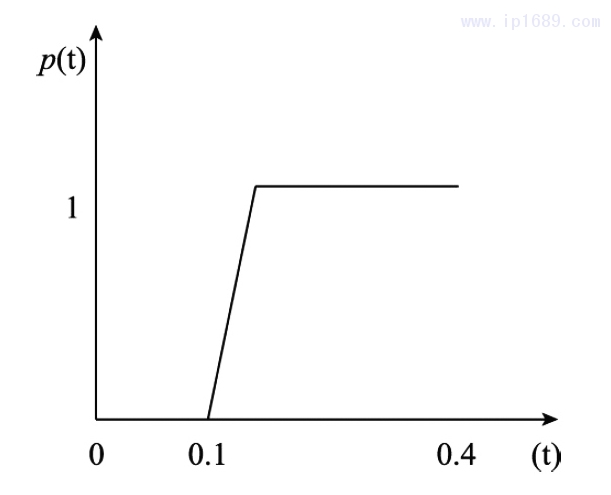
图 4 压力斜坡函数
吹胀压力P(t)同样采用渐进函数—斜坡函数实现[11]。其中,斜坡函数参数如图 4 所示。
2.2. 2 数值模拟结果
吹塑过程包括模具合模挤压型坯和吹塑膨胀2个阶段[12]。图5为A1B1C1挤出吹塑过 程,由图可知,型坯厚度的变化规律。
此方案吹塑总时间为2s。由图5可知,吹胀前段时间,型坯形状变化较明显,1.33s后,厚度变化较小。等厚度型坯接触模具的同时,温度降低,黏度变大,变形程度较小,厚度变化程度较小[13]。所以先接触模具的型坯厚度较大[14]。相反,后接触模具的拐角位置继续变形,厚度不断减小,因而形成厚度不均匀的情况[15]。
2.3 结果与讨论
2.3. 1 厚度分析
最优的制品壁厚分布是评价制品质量最重要的指标之一[16]。12点大致位于瓶身的两条对称线上,并根据多次模拟结果得出规律12处是局部厚度的转折点,即较厚或较薄的位置。采用局部特征代表整体均匀性的方法,具有代表性[17]。表6、图6均为12个特征点的空间位置。

图 5 A1B1C1 方案吹塑过程
(a)0. 01 s (b)0. 25 s (c)0. 31 s (d)1. 33 s
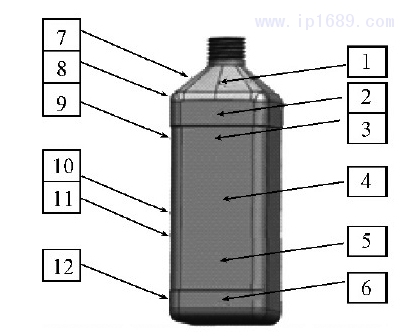
图 6 12 个特征点的空间位置
表 2 12 个特征点的空间位置
图7为9组工艺参数12个位置的壁厚变化曲线,虚线代表各壁厚均值。从图中可以看到成型制件每点壁厚与均值的偏离程度,偏离程度越小,制件壁厚之间的差异越小;偏离程度越大,制件壁厚之间的差异越大[18]。
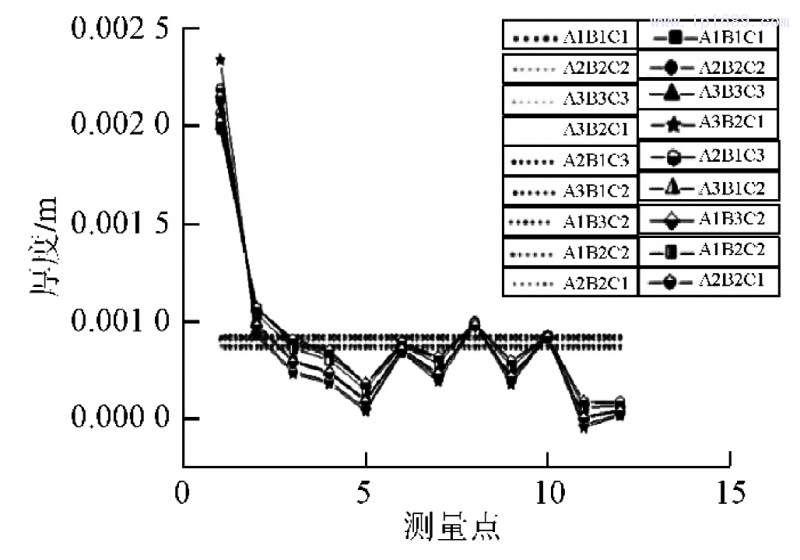
图 7 9 种方案的 12 个位置的厚度分布情况
12个点的厚度根据均值分为3个水平,点1、2处厚度均大于1 mm;点5、11、12处厚度较薄,点11处只有0.534mm;其余特征点厚度均值在0. 7~1 mm。从图7中可以看出,A1B1C1、A2B2C2、A3B3C3组中,大部分特征点的壁厚值均在均值以上波动,其余方案则在均值以下波动。A3B1C2组的壁厚值在均值附近波动的频率是最均匀的。
由图8可知,除位置1的厚度较大外,其他位置均在0. 5~1mm 范围内,工艺参数对位置 6、10处厚度变化的影响较小,且不同组合的变化趋势较为相似,而且,其变形量的变化趋势也基本一致。
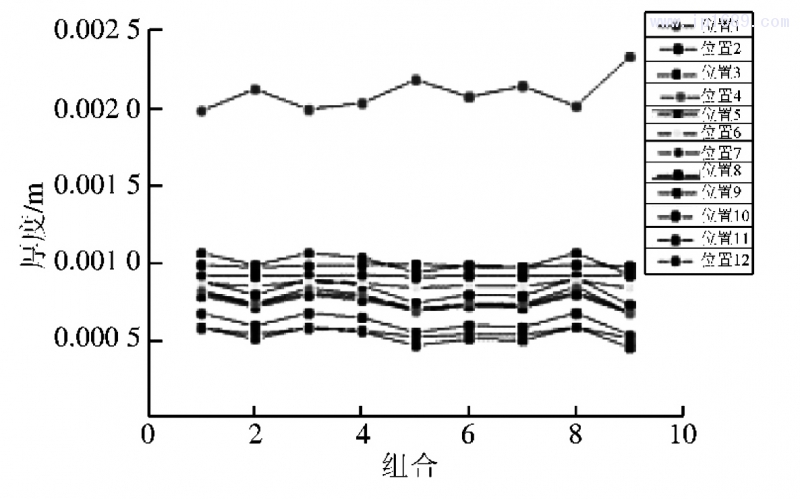
图 8 12 个位置不同参数组合下的厚度分布情况
2.3. 2 方差分析
9组正交试验的结果如表3所示,分析了12个特征点的壁厚方差值以及壁厚的均匀性情况。通过极差分析,影响权重为因素B<A<C。
图9为采用二次方程拟合的曲线,拟合度为0.99,预测值与实际值较为一致。最终得到试验最优工艺参数,吹胀压力为0. 456 MPa,吹胀时间为1.210 s,模具运动速度为0.878 m/s。
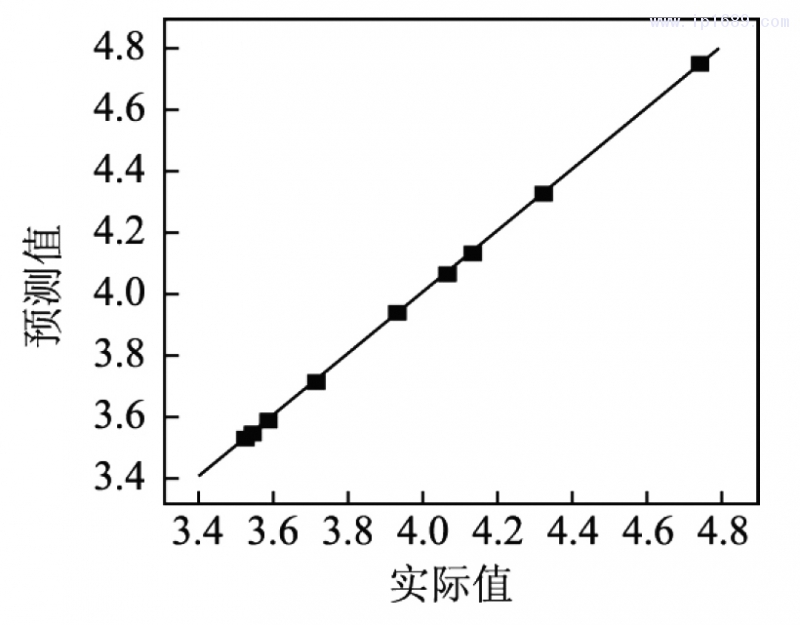
图 9 预测值与实际值的对比
3 非等厚度型坯优化
型坯成型过程中,只有拉伸没有压缩变形,因此,变形量δ=H型坯/H制件,H型坯为某位置初始型坯厚度,H制件为同一位置制件的厚度[19]。如瓶口部分初始型坯厚度为1mm,得到的制件为1mm,通过公式得到变形量δ=1。同理,得到13段厚度的
变形量。假设每段理想制件厚度为1.8 mm,则H理想型坯=H理想制件×δ,最终确定13段非等厚度理想型坯的厚度值[20],如图 10 所示。
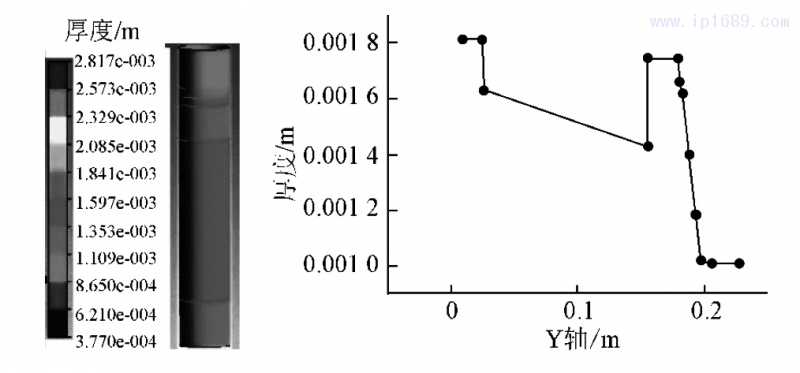
图 10 13 段非等厚度型坯及各段厚度值
4 生产验证
通过正交实验结果得出了最优工艺参数,经过13段非等厚度理想型坯吹胀成型,壁厚方差为1. 94×10-4m2,小于正交试验的最小方差3.52762×10-4m2,壁厚均匀性显著提高,壁厚平均值为0.773 mm,最低厚度为0.556 mm,厚度合格。最终优化模型与产品如图 12 所示。
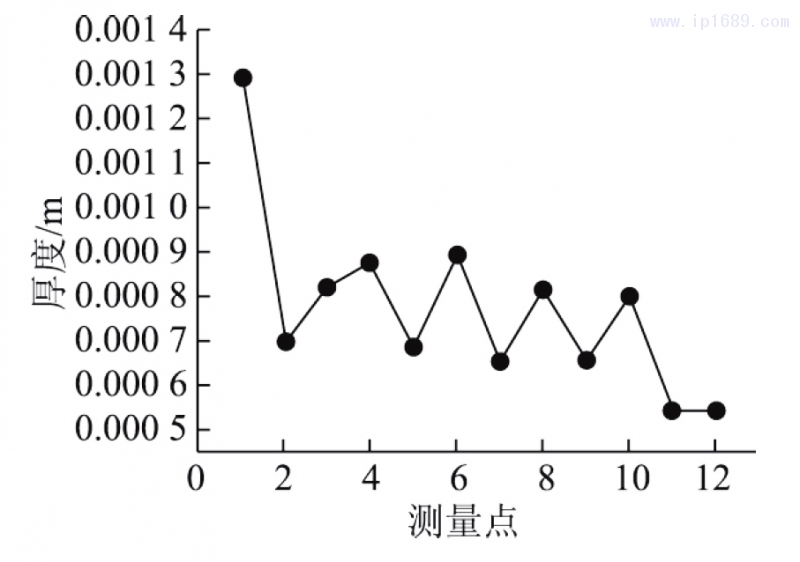
图 11 制件的 12 个点壁厚值

图 12 模型与制品图
5 结论
(1)正交实验为优化制件壁厚实验提供了合理的工艺参数[21]。通过三因素三水平正交试验,借助Polyflow软件模拟9组方案的挤出吹塑过程,取12组特征位置的制品壁厚值,经过方差分析,得到1 L墨水瓶的吹塑工艺最优参数,吹胀压力为0.456MPa、吹胀时间为1.210 s、模具运动速度为0.878 m/s。
(2)通过正交试验法得到最优工艺参数,用于指导非等厚度型坯的模拟与生产,进一步提高了产品壁厚均匀性。
参考文献:
[1]王海民.挤出吹塑成型中压力的变化对中空工业制件壁厚的影响[D].重庆:重庆理工大学,2010.
[2]任清海,翁楠,耿铁.注塑制品翘曲变形的影响因素及对策[J].塑料制造,2015(5):69 -72.
[3]张振,朱元吉.基于Polyflow的塑料异型材挤出模头功能块流道的设计[J].模具工业,2007(7):61-64.
[4]顾菲菲,朱志松,严晓照.吨包装内胆挤出吹塑成型型坯吹胀的数值模拟[J].现代塑料加工应用,2013,25(1):46-49.
[5]黄虹,王海民,邱方军,等.挤出吹塑塑料油箱壁厚均匀性的研究与应用[J].塑料科技,2010,38(2):62-65.
[6]黄虹,邱方军,王海民,等.口模异型化设计在优化挤出吹塑中空工业制件壁厚分布中的研究与应用[J].工程塑料应用,2009,37(12):68-71.
[7]丁小锋,范存金,周利军,等.10 mL PP塑料瓶吹塑成型过程仿真分析[J].机电信息,2017(26):22-27.
[8]钟世云.中空吹塑制品的新进展[J].中国塑料,2003,17 (8 ):9-14.
[9]黄汉雄.工程塑料挤出吹塑的机械与工艺[J].工程塑料应用,1991(3):33-36.
[10 李海梅,高峰,申长雨.吹塑成型发展现状[J].塑胶工业,2006(3):15-19.
[11 李道喜,李能文,明浩,等.改善挤出吹塑制件壁厚均匀性的几种方法[J].精密成形工程,2012,4(1):54-57.
[12]钱欣,许王定,金杨福.POLYFLOW 基础及其在塑料加工中的应用[M].北京:化学工业出版社,2010.
[13]DEBBAUT B,HOMERIN O,JIVRAJ N.A comparison betweenexperiments and predictions for the blow molding of an industrial part
[J].Polymer Engineering and Science,1999,39(9):1812-1822.
[14]吴其晔,巫静安.高分子材料流变学[M].北京:高等教育出版社,2002.
[15]易婷,焦志伟,杨卫民.挤出吹塑成型初始型坯温度的数值模拟优化[J].塑料,2016,45(6):69 - 72.
[16]郝晨晖,王婷.中空吹塑成型技术专利分析[J].河南科技,2016(22):56 -58.
[17]黄虹,李军,陈元芳,等.中小型中空塑件的多管坯挤出吹塑成型技术研究[J].工程塑料应用,2004,32(4):20-24.
[18]PEPLISKI K,MOZERA.Ansys-Polyflow software use to selec the parison diameter and its thickness distribution in blowing extrusion
[J].Journal of Polish CIMAC,2010,5(3):133-142.
[19]苏龙.对高分子材料的加工成型技术研究[J].信息记录材料,2017,18(5):43-44.
[20]黄虹,刘春,黄强.中空塑件单管坯挤出-多型腔吹塑工艺研究[J].中国塑料,2004,18(7):54-57.
[21] WANG J,PENG J,CHEN J,et al.Numerical Optimization of theparison thickness of oil drum in extrusion blow molding[J].Advanced Materials Research,2014,881 /882 /883:1455-1459.










 玻纤含量对长玻纤...
玻纤含量对长玻纤... 钙钛矿薄膜的均匀...
钙钛矿薄膜的均匀... 用于光伏板静电除...
用于光伏板静电除... 聚砜医疗干粉吸入...
聚砜医疗干粉吸入...













