王浩1,王继先2
1平顶山技师学院,河南平顶山467000
2河南化工技师学院,河南开封475004
摘 要:为提高注塑机液压伺服控制系统的精确度和稳定性,提出了基于量子遗传算法的注塑机PID控制系统。引入量子遗传算法对注塑机PID系统参数进行全局寻优,以累积误差作为目标函数,根据实际工况动态调节PID参数。仿真实验和实测分析结果表明,本控制系统在精度和稳定性上优于传统PID控制方法,且超调量更小、运算速度更快,有效确保了产品质量的一致性。
关键词:注塑机;液压系统;PID;量子遗传算法
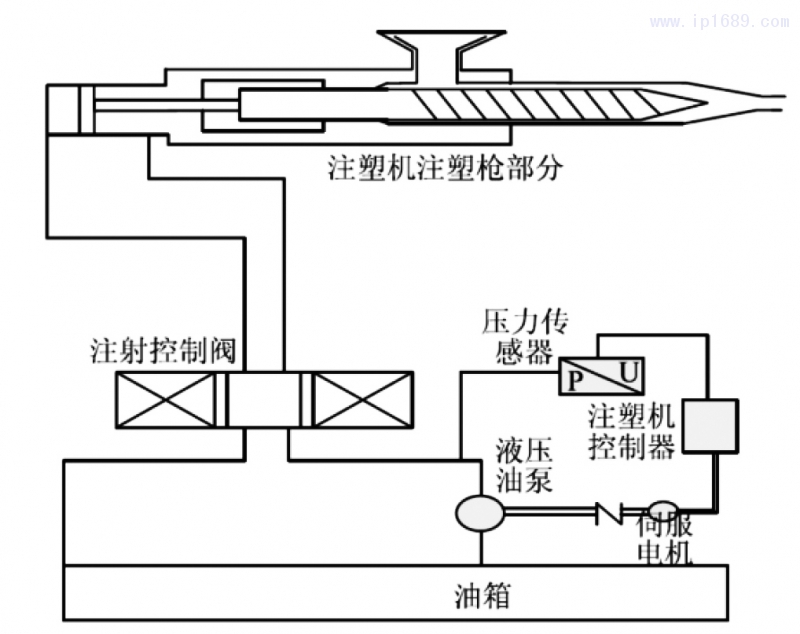
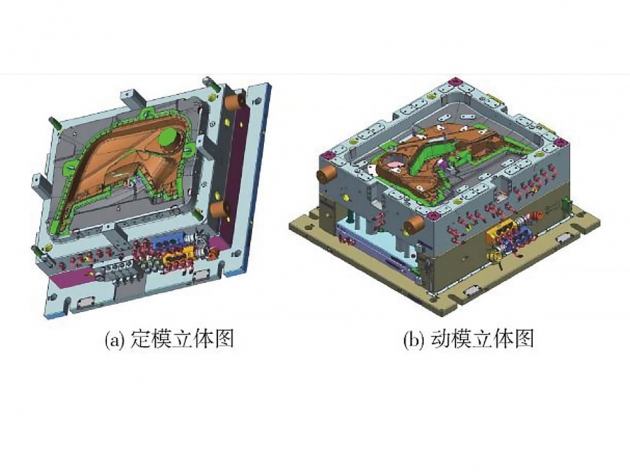
液压系统是注塑机的重要组成部分,液压控制系统直接关系到塑料制品的质量和性能[1-3]。图1为注塑机伺服闭环控制系统,该系统包含伺服电机、液压泵、液压阀等器件,与注塑产品生产紧密关联。为保证注塑机稳定工作,注塑机液压伺服系统主要采用PID闭环控制技术进行反馈调节。文献[4]将PID与神经网络融合,实时调节液压控制系统相关参数,显著提高了注塑制品的尺寸精度;文献[5]使用PID分段控制液压系统,提高了注塑机控制精度,克服了PID固定参数引起控制精度下降的问题;文献[6]结合变论域与自适应模糊PID控制理论设计了控制系统,显著提高了注塑机液压系统的动态性能。上述方案均具有自动调节能力,大幅提升了注塑制品的质量和生产效率,但是在参数选择上仍然不够快速灵活,存在调节时间过长等问题。
近年来,量子理论与经典优化算法的结合得到了国内外学者的广泛关注。文献[7]将量子理论与遗传算法结合,进一步提高了遗传算法的收敛速度,解决了敏捷成像卫星调度问题;文献[8]将量子理论应用于菌群算法,以更快的速度完成了PID参数整定;文献[9]运用量子理论改进粒子群优化算法,获得了更快的寻优速度。上述研究表明,量子优化算法具有更快的寻优速度、更高的寻优精度,适用于解决多参数全局寻优问题。
注塑机液压系统的PID控制系统参数关系到注塑制品质量,根据反馈信息对液压伺服系统的控制参数进行动态调整,有利于提高系统的稳定性。因此,本文引入量子遗传算法实时调节液压伺服系统的PID参数,以克服不确定因素带来的干扰,提升注塑机在生产过程的自适应能力。
1问题描述
在生产过程中,注塑机液压伺服系统一方面要保证较高的响应速度,根据外界环境变化和产品生产过程及时调节;另一方面还要确保较高的控制精度,参数调节必须能够反应真实的生产需求。塑料融化过程中,压力处于时刻变化状态,需要对压力进行及时响应;熔料流入压力枪后,一旦出现压力不均衡的情况,将引起熔料在注塑枪内回流,对注塑制品质量产生严重影响。综上,必须使用具有全局快速寻优能力的算法对液压系统进行实时控制。
2量子遗传算法
2.1量子编码
与其他优化算法不同,量子遗传算法使用量子比特来表示种群中的每一个个体。在量子理论中,量子比特的表达式为:
式(1)中,|0〉、|1〉称为量子比特的基态,α和β分别表示对应基态的量子概率幅。量子比特的量子概率幅在数学上必须满足约束条件:
由式(2)可得,α,β∈[-1,1]。
n维寻优问题可以表达为:
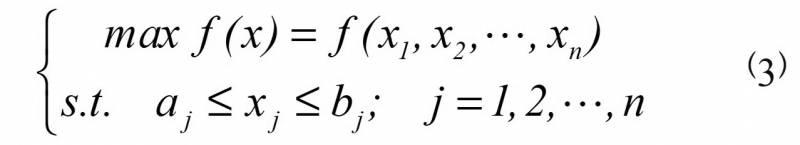
式(3)中,X=(x1,x2,…,xn)T∈Rn,为n维寻优问题的最优解,aj和bj表示最优解X的第j个变量xj的临界值。量子遗传算法使用式的量子概率幅对个体进行编码:
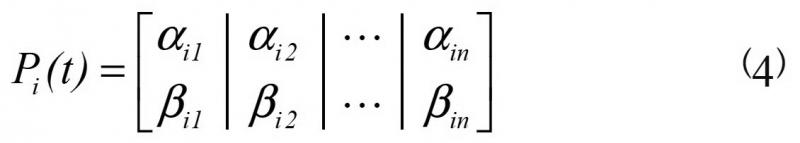
Pi(t)表示第t代种群中第i个个体。由于图片|cos(x)|2+|sin(x)|2=1,满足式(2)约束条件,故使用sin和cos函数对式(4)进一步表达:
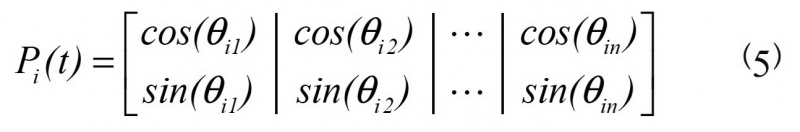
式(5)中,θij表示角度,θij=2π×rnd,rnd为[-1,1]范围内的实数;i=1,2,…,m,表示种群个体;j=1,2,…,n,表示个体的量子比特。式(5)表明,对于一个n维的寻优问题,每一个个体需要使用n个量子比特。由此可得,n维寻优问题实际上是在n维量子空间In=[−1,1]n内部搜索最优解的过程。
对于任意实数而言,如果用余弦进行表示,必然存在2个角度与之对应;如果用正弦进行表示,同样存在2个角度与之对应。因此对于一个实数必然存在4个角度值在量子空间与之对应。对于n维的寻优问题而言,如果实数空间Rn存在M个全局最优解,在n维量子空间In=[−1,1]n中对应有4nM=2n+1M个最优解[10-11]。这一结论表明,将实数空间的解映射到量子空间,全局最优解将以指数倍数增加,极大增加了搜索到最优解的概率。
2.2个体进化
量子遗传算法的个体进化更新时,主要通过对自身量子比特概率幅进行改变,通常通过量子旋转门完成:
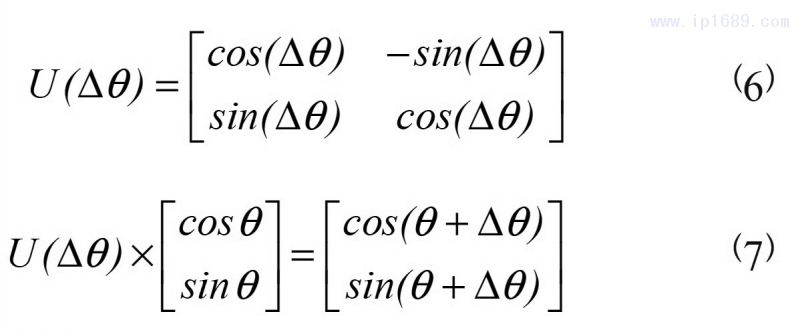
Δθ为量子进化算法中的个体转角步长,其取值大小直接关系到量子进化算法的搜索能力。Δθ过小容易陷入局部最优解,不利于全局最优解寻找;Δθ过大能提高搜索速度,但会降低精度,影响控制对象的性能。
2.3个体变异
在保证精度的前提下,如果只采用个体进化,往往难以跳出覆盖范围较大的局部最优解。因此,在进化过程中必须选择个体进行变异,大幅改变个体的量子比特状态,与当前种群形成显著差异。可采用量子非门完成个体变异:
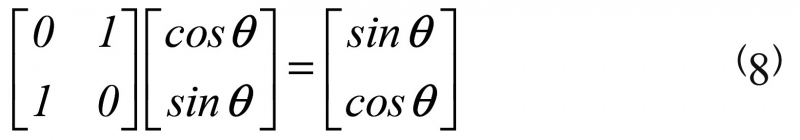
经过量子非门转换,结合式(4)和式(5)可知,此时量子比特的量子概率幅进行了调换,极大改变了量子比特状态,有助于摆脱当前种群局限,提高全局搜索能力。
2.4解空间变换
量子比特寻找最优解范围在[-1,1]区间,必须将[-1,1]映射回实数空间才能得出最终结果。结合式(2),可以分别使用α和β将量子空间的值换算为实数空间解。根据式(3)可知:
(1)如果使用基态|0〉的量子概率幅α,则实数空间中最优解X的第j位转换式为:
(2)如果使用基态|1〉的量子概率幅β,则实数空间中最优解X的第j位转换式为:
综上,量子遗传算法的个体使用量子编码,但进化过程与传统的遗传算法基本一致,由于具有更多的全局最优解,因此其搜索速度更快,一定程度上避免了陷入局部最优解。
3 PID控制系统
基于量子遗传算法的注塑机PID控制系统如图2所示。
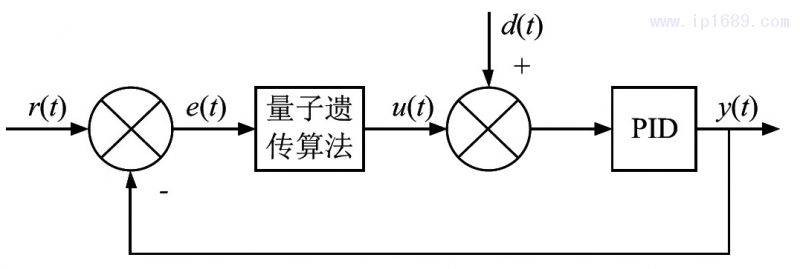
PID控制系统的输入输出关系为:
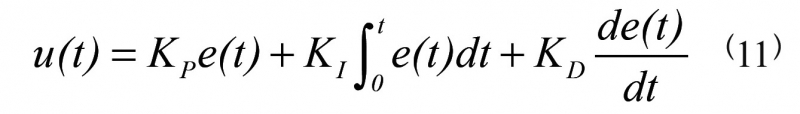
量子遗传算法用于对式(11)中的三个参数KP、KI、KD进行寻优。由于系统具有滞后性,无法使用瞬时误差e(t)判断当前参数是否为最优参数,本文采用累积误差作为目标函数:

4实验分析
4.1 仿真分析
利用MATLAB的Simulink对本文所提PID控制系统进行测试,信号输入为阶跃信号。参数设置参考200T注塑机,具体参数如表1所示。
图3为仿真实验结果,仿真时间10s,系统输入为1。传统PID系统根据经验将三个参数设置为KP=2、KI=0.08、KD=0.03。从图3可以看出,基于量子遗传算法的注塑机PID控制系统超调量更小,输出波动更小。与传统PID相比,量子优化PID系统的参数随着反馈动态调节,输出控制更加平稳,调节速度更快,有利于保证产品质量。
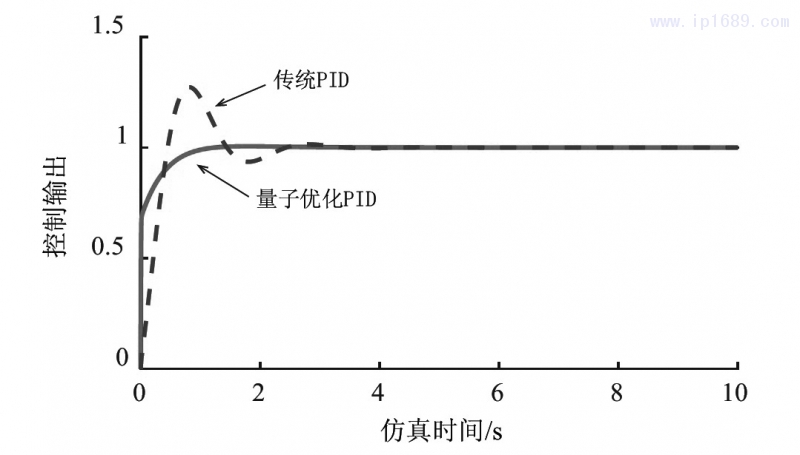
4.2实测分析
以200T伺服型注塑机进行实测分析。起始位置设置为31mm,注塑完毕位置设置为80mm,表2为注塑前后螺杆位置对比。
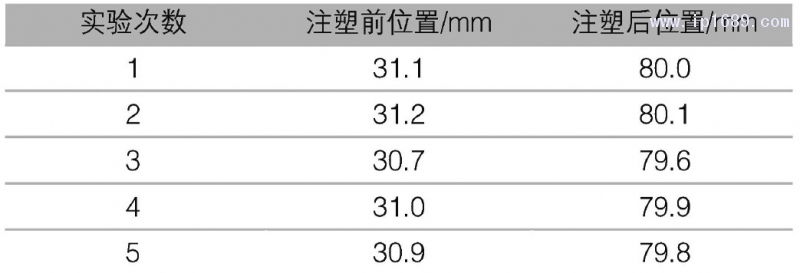
从表2可以看出,注塑前螺杆的位置最大值为31.2mm,最小值为30.7mm;注塑后螺杆的位置最大值为80.1mm,最小值为79.6mm。误差均在1%以内,说明本文提出的控制系统具有较高精度。
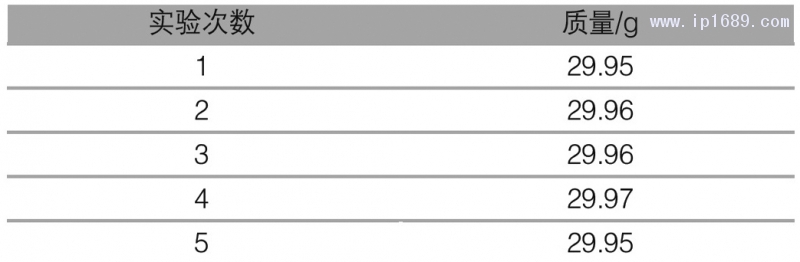
以30g注塑产品为例检测其质量,结果如表3所示。从表3可以看出,所有产品质量误差均在1%以内,说明基于量子遗传算法的注塑机PID控制系统具有良好的稳定性,能充分保证产品质量的一致性。
5结论
将量子遗传算法引入传统PID控制,动态调节注塑机液压伺服系统的PID控制参数,有效提高了控制系统的精确度和稳定性。量子遗传算法具有较高的全局寻优能力,能够针对外部环境变化和产品生产反馈信息实时调整参数。与传统PID控制系统相比,基于量子遗传算法的注塑机PID控制系统能够以较小的超调量、较快的运算速度获得质量稳定的注塑制品,为注塑机控制提供了一种有效途径。
参考文献:
[1] 焦志伟,安瑛,谢鹏程,等.新型注塑机合模机构内循环节能机理[J].机械工程学报,2012,48(10):153-159.
[2] 曾广胜,瞿金平,江太君,等.一种注塑机锁模系统的理论计算与模拟分析[J].高分子材料科学与工程,2012,28(2):169-173.
[3] 刘浩.注塑机领域的研究进展[J].合成树脂及塑料,2018,35(4):99-102.
[4] 党霞.基于自适应神经网络PID的注塑机温度控制[J].合成树脂及塑料,2018,35(6):83-86.
[5] 陶西孟,罗亮,刘知贵.基于分段PID的注塑机料筒温度控制算法研究与仿真[J].塑料,2015,44(3):68-70.
[6] 张鹏,冯显英,霍睿,等.基于变论域自适应模糊PID的注塑机温控系统研究[J].组合机床与自动化加工技术,2017(7):107-109,115.
[7] 王海蛟,贺欢,杨震.敏捷成像卫星调度的改进量子遗传算法[J].宇航学报,2018,39(11):1266-1274.
[8] 刘璐,单梁,戴跃伟,等.非线性动态自适应旋转角的量子菌群算法[J].控制与决策,2017,32(12):2137-2144.
[9] 张艺瀛,金志刚.一种高维多模态优化的量子粒子群优化算法[J].哈尔滨工业大学学报,2018,50(11):50-58,82.
[10] 刘志刚,许少华,李盼池,等.基于量子衍生布谷鸟的脊波过程神经网络及TOC预测[J].控制与决策,2017,32(6):1115-1120.
[11] 张强,李盼池,刘丽杰.基于量子混合蛙跳算法的油田开发规划多目标优化[J].信息与控制,2014,43(1):116-122.









 玻纤含量对长玻纤...
玻纤含量对长玻纤... 钙钛矿薄膜的均匀...
钙钛矿薄膜的均匀... 用于光伏板静电除...
用于光伏板静电除... 聚砜医疗干粉吸入...
聚砜医疗干粉吸入...













